
【题目】如图,多面体![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上的点.
上的点.
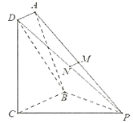
(Ⅰ)若![]() 平面
平面![]() ,证明:
,证明:![]() 是
是![]() 的中点;
的中点;
(Ⅱ)若![]() ,
,![]() ,求二面角
,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)利用线面平行的性质定理,可以证明出![]() ,
,![]() ,利用平行公理可以证明出
,利用平行公理可以证明出![]() ,由中位线的性质可以证明出N是DP的中点;
,由中位线的性质可以证明出N是DP的中点;
(Ⅱ)方法1:在平面ABCD中作![]() 于垂足G,过G作
于垂足G,过G作![]() 于H,连接AH,利用面面垂直和线面垂直,可以证明出
于H,连接AH,利用面面垂直和线面垂直,可以证明出![]() 为二面角
为二面角![]() 的平面角,在直角三角形中,利用锐角三角函数,可以求出二面角
的平面角,在直角三角形中,利用锐角三角函数,可以求出二面角![]() 的平面角的余弦值;
的平面角的余弦值;
方法2:由平面![]() 平面PBC
平面PBC![]() ,可以得到
,可以得到![]() 平面PBC,
平面PBC,![]() ,
,
而![]() 即
即![]() ,于是可建立如图空间直角坐标系(C为原点),利用空间向量的数量积,可以求出二面角
,于是可建立如图空间直角坐标系(C为原点),利用空间向量的数量积,可以求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
(I)设平面![]() 平面
平面![]() ,
,
因为![]() 平面PBC,
平面PBC,![]() 平面ADP,所以
平面ADP,所以![]() ,
,
又因为![]() ,所以
,所以![]() 平面PBC,
平面PBC,
所以![]() ,
,
所以![]() ,
,
又因为M是AP的中点,所以N是DP的中点.
(II)方法1:
在平面ABCD中作![]() 于垂足G,
于垂足G,
过G作![]() 于H,连接AH(如图),
于H,连接AH(如图),
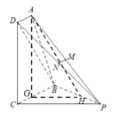
因为平面![]() 平面PBC,
平面PBC,![]() ,
,
所以![]() 平面PBC,
平面PBC,![]() ,
,![]() ,
,![]() ,
,
所以![]() 平面PBC,
平面PBC,![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角,
的平面角,
易知![]() ,
,![]() ,又
,又![]() ,
,
所以在![]() 中,易知
中,易知![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
(II)方法2:
因为平面![]() 平面PBC
平面PBC![]() ,
,
所以![]() 平面PBC,
平面PBC,![]() ,
,
而![]() 即
即![]() ,
,
于是可建立如图空间直角坐标系(C为原点),
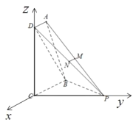
得![]() ,
,![]() ,
,![]() ,
,
所有![]() ,
,![]() ,
,
设平面APB的法向量为![]() ,则
,则
![]() ,
,![]() ,
,
不妨取![]() ,得
,得![]() ,
,
可取平面PBC的法向量为![]() ,
,
所求二面角![]() 的平面角为
的平面角为![]() ,则
,则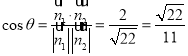 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点A
过点A![]() ,两个焦点为(-1,0),(1,0)。
,两个焦点为(-1,0),(1,0)。
(Ⅰ)求椭圆C的方程;
(Ⅱ)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明.下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用![]() ,化简,得
,化简,得![]() .设勾股形中勾股比为
.设勾股形中勾股比为![]() ,若向弦图内随机抛掷
,若向弦图内随机抛掷![]() 颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为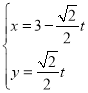 ,(
,(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程和圆
的极坐标方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为圆
为圆![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F且EF=![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
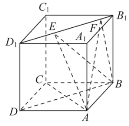
A.AC⊥BEB.EF![]() 平面ABCD
平面ABCD
C.三棱锥A-BEF的体积为定值D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,侧面PAD是边长为2的等边三角形且垂直于底![]() ,
, ![]()
![]() 是
是![]() 的中点。
的中点。
(1)证明:直线![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了庆祝第一个农民丰收节,西部山区某村统计了自2011年以来每年的年总收入,其中2018年统计的是1月到8月的总收入,统计结果如图所示.根据图形,下列四个判断中,错误的是( )
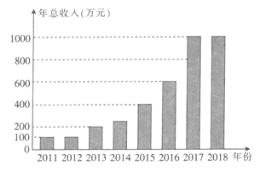
A.从2012年起,年总收入逐年增加B.2017年的年总收入在2016年的基础上翻了番
C.年份数与年总收入成正相关D.由图可预测从2014年起年总收入增长加快
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com