
(本小题满分12分)
已知函数 ,
,
(1) 若存在实数 ,使得
,使得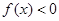 ,求实数
,求实数 的取值范围;
的取值范围;
(2) 设 ,且
,且 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。
(1)存在实数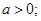 或
或 ;(2)
;(2) 。
。
解析试题分析:(1)直接零函数小于零,解一元二次不等式即可
(2)根据 ,且
,且 在区间
在区间 上单调递增,那么可知对于参数a进行分类讨论得到结论。
上单调递增,那么可知对于参数a进行分类讨论得到结论。
解:(1)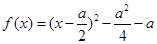 ,当仅当
,当仅当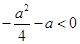 时,存在实数
时,存在实数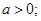 或
或 …………………3分
…………………3分
(2)当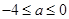 时,
时, 在
在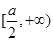 上递增,则
上递增,则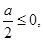 即
即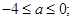 …………………5分
…………………5分
当 或
或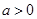 时,设
时,设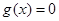 的两根为
的两根为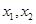 ,且
,且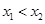 ,此时
,此时 在区间
在区间 或
或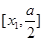 上递增。…………………7分。
上递增。…………………7分。
若 ,则
,则 ,得
,得 ;…………………9分
;…………………9分
若 ,则
,则 ,得
,得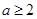 ,…………………11分
,…………………11分
综上可知, 的取值范围是
的取值范围是 …………………12分。
…………………12分。
考点:本试题主要考查了一元二次不等式的求解以及函数单调性的运用。
点评:解决该试题的关键是根据已知条件得到二次不等式,结合二次函数性质得到结论。同时对于绝对值函数,要分类去掉其符号。


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
(本小题15分)已知函数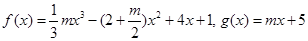 .
.
(1)当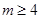 时,求
时,求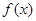 的单调递增区间;
的单调递增区间;
(2)是否存在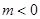 ,使得对任意的
,使得对任意的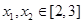 ,都有
,都有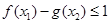 恒成立.若存在,求出
恒成立.若存在,求出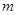 的取值范围; 若不存在,请说明理由.
的取值范围; 若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)经市场调查,某种商品在过去50天的销售量和价格均为销售时间t(天)的函数,已知前30天价格为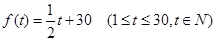 ,后20天价格为f(t)="45" (31£ t £50, tÎN),且销售量近似地满足g(t)=" -2t+200" (1£t£50, tÎN).
,后20天价格为f(t)="45" (31£ t £50, tÎN),且销售量近似地满足g(t)=" -2t+200" (1£t£50, tÎN).
(I)写出该种商品的日销售额S与时间t的函数关系式;
(II)求日销售额S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)星期天,刘先生到电信局打算上网开户,经询问,记录了可能需要的三种方式所花费的费用资料,现将资料整理如下:
1163普通:上网资费2元/小时;
2163A:每月50元(可上网50小时),超过50小时的部分资费2元/小时;
3ADSLD:每月70元,时长不限(其他因素忽略不计).
请你用所学的函数知识对上网方式与费用问题作出研究:
(1)分别写出三种上网方式中所用资费与时间的函数解析式;
(2)在同一坐标系内分别画出三种方式所需资费与时间的函数图象;
(3)根据你的研究,请给刘先生一个合理化的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com