
分析 由题意可得c-$\frac{{a}^{2}}{c}$=2a,化简整理,结合离心率公式,即可得到所求值.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$的焦点(c,0)到相应准线x=$\frac{{a}^{2}}{c}$的距离等于实轴长2a,
可得c-$\frac{{a}^{2}}{c}$=2a,即c2-2ac-a2=0,
解得c=(1+$\sqrt{2}$)a或c=(1-$\sqrt{2}$)a(舍去),
即有离心率e=$\frac{c}{a}$=1+$\sqrt{2}$.
故答案为:1+$\sqrt{2}$.
点评 本题考查双曲线的几何性质的运用,主要考查准线和离心率的求法,考查运算能力,属于中档题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
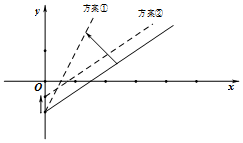 如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )
如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )| A. | 方案①降低成本,票价不变,方案②提高票价而成本不变; | |
| B. | 方案①提高票价而成本不变,方案②降低成本,票价不变; | |
| C. | 方案①降低成本,票价提高,方案②提高票价而成本不变; | |
| D. | 方案①提高成本,票价不变,方案②降低票价且成本降低 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (-1,3) | C. | (3,5) | D. | (-1,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{25}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,sinx<0 | B. | ?x∈R,sinx≤0 | C. | ?x∈R,sinx≤0 | D. | ?x∈R,sinx<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com