
【题目】如图,已知长方形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
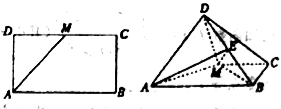
(1)求证:![]() ;
;
(2)若点![]() 是线段
是线段![]() 上的一动点,问点
上的一动点,问点![]() 在何位置时,三棱锥
在何位置时,三棱锥![]() 的体积与四棱锥
的体积与四棱锥![]() 的体积之比为1:3?
的体积之比为1:3?
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】某公司生产一批![]() 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批![]() 产品所需原材料减少了
产品所需原材料减少了![]() 吨,且每吨原材料创造的利润提高了
吨,且每吨原材料创造的利润提高了![]() ;若将少用的
;若将少用的![]() 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的![]() 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为![]() 万元,其中
万元,其中![]() .
.
(1)若设备升级后生产这批![]() 产品的利润不低于原来生产该批
产品的利润不低于原来生产该批![]() 产品的利润,求
产品的利润,求![]() 的取值范围;
的取值范围;
(2)若生产这批![]() 产品的利润始终不高于设备升级后生产这批
产品的利润始终不高于设备升级后生产这批![]() 产品的利润,求
产品的利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:关于x的方程x2+ax+2=0无实根,命题q:函数f(x)=logax在(0,+∞)上单调递增,若“p∧q”为假命题,“p∨q”真命题,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某河上有座抛物线型拱桥,当水面距拱顶5m时水面宽为8m,一木船宽为4m,高为2m,载货后木船露在水面上的部分高为0.75m,问水面上涨到与拱顶相距多少时,木船开始不能通过。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,已知
,已知![]() 在
在![]() 处的切线
处的切线![]() 相同.
相同.
(1)求![]() 的值及切线
的值及切线![]() 的方程;
的方程;
(2)设函数![]() ,若存在实数
,若存在实数![]() 使得关于
使得关于![]() 的不等式
的不等式![]() 对
对![]() 上的任意实数
上的任意实数![]() 恒成立,求
恒成立,求![]() 的最小值及对应的
的最小值及对应的![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() :
:![]() ,设圆
,设圆![]() 的半径为1,圆心在
的半径为1,圆心在![]() 上.
上.
(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某加工厂需定期购买原材料,已知每公斤原材料的价格为1.5元,每次购买原材料需支付运费600元,每公斤原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400公斤,每次购买的原材料当天即开始使用(即有400公斤不需要保管).
(Ⅰ)设该厂每x天购买一次原材料,试写出每次购买的原材料在x天内总的保管费用y1关于x的函数关系式;
(Ⅱ)求该厂多少天购买一次原材料才能使平均每天支付的总费用y最少,并求出这个最少(小)值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个盒子里装有6张卡片,上面分别写着如下定义域为![]() 的函数:
的函数:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)现在从盒子中任意取两张卡片,记事件![]() 为“这两张卡片上函数相加,所得新函数是奇函数”,求事件
为“这两张卡片上函数相加,所得新函数是奇函数”,求事件![]() 的概率;
的概率;
(2)从盒中不放回逐一抽取卡片,若取到一张卡片上的函数是偶函数则停止抽取,否则继续进行,记停止时抽取次数为![]() ,写出
,写出![]() 的分布列,并求其数学期望
的分布列,并求其数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com