【题目】函数
在区间
上的最大值记为
．
（1）求的解析式；
（2）求的最大值．
【答案】（1）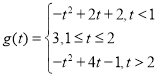 
；（2） 3
【解析】
试题分析：（1）对区间
与对称轴
的位置关系进行讨论，即分为①t<1时；②当1≤t≤2时；③当t>2时三种情况（2） 作出分段函数图象，即可求出求最大值.
试题解析：解：（1）对区间[t，t＋1]（t∈R）与对称轴x＝2的位置关系进行讨论：①当t＋1<2，
即t<1时，函数f（x）在区间[t，t＋1]上递增，此时
；
②当t≤2≤t＋1，即1≤t≤2时，函数f（x）在区间[t，t＋1]上先增后减，此时g（t）＝f（2）＝3；
③当t>2时，函数f（x）在区间[t，t＋1]上递减，此时
.
综上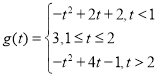， ……7分
（2） 分段求最大值得g（t）的最大值是3. ……5分
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目：高中数学 来源： 题型：
【题目】下列关于用斜二测画法画直观图的说法中，正确的是( )
A.水平放置的正方形的直观图不可能是平行四边形
B.平行四边形的直观图仍是平行四边形
C.两条相交直线的直观图可能是平行直线
D.两条垂直的直线的直观图仍互相垂直
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法中正确的个数是（ ）
①若直线l与平面α内的一条直线垂直，则l⊥α；
②若直线l与平面α内的两条直线垂直，则l⊥α
③若直线l与平面α内的两条相交直线垂直，则l⊥α；
④若直线l与平面α内的任意一条直线垂直，则l⊥α.
A.4
B.2
C.3
D.1
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设某厂产品的次品率为2%,估算该厂8 000件产品中合格品的件数大约为( )
A. 160 B. 7 840
C. 7 998 D. 7 800
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义：“对于函数f（x），若存在x0，使f（x0）＝x0成立，则称x0为函数f（x）的不动点。”已知f（x）＝x2＋bx＋c.
（1）若f（x）有两个不动点为－3,2，求函数f（x）的零点．
（2）当c＝
b2时，函数f（x）没有不动点，求实数b的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
