
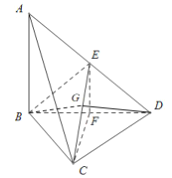
【题目】如图,在四面体![]() 中,E是线段
中,E是线段![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
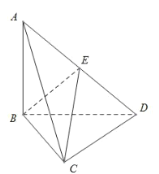
(1)证明:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .证明
.证明![]() .推出
.推出![]() 平面
平面![]() ,然后证明
,然后证明![]() .
.
(2)解法一:令![]() ,点
,点![]() 为原点,射线
为原点,射线![]() 、
、![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴正方向,建立空间直角坐标系,如图所示.求出平面
轴正方向,建立空间直角坐标系,如图所示.求出平面![]() 、平面
、平面![]() 的法向量,利用空间向量的数量积求解平面
的法向量,利用空间向量的数量积求解平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
解法二:令![]() ,取
,取![]() 中点
中点![]() ,则
,则![]() ,
,![]() ,说明
,说明![]() 为二面角
为二面角![]() 的平面角,利用余弦定理转化求解,平面
的平面角,利用余弦定理转化求解,平面![]() 与平面
与平面![]() 所成锐二面角的余弦值即可.
所成锐二面角的余弦值即可.
(1)取线段![]() 的中点F,连接
的中点F,连接![]() 、
、![]() .
.
因为E是线段![]() 的中点,所以
的中点,所以![]() .又
.又![]() ,所以
,所以![]() .
.
因为![]() ,F是
,F是![]() 的中点,所以
的中点,所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
所以![]() .
.
(2)解法一:
令![]() ,则
,则![]() ,
,
那么![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
又![]() ,
,![]() ,故可以以点F为原点,射线
,故可以以点F为原点,射线![]() 、
、![]() 、
、![]() 分别为x轴、y轴、z轴正方向,建立空间直角坐标系,如图所示.
分别为x轴、y轴、z轴正方向,建立空间直角坐标系,如图所示.
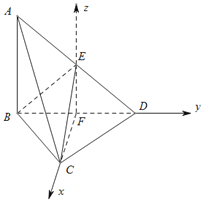
则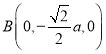 ,
, ,
,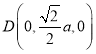 ,
, ,
,
所以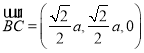 ,
,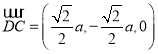 ,
, .
.
设平面![]() 、平面
、平面![]() 的法向量分别为
的法向量分别为![]() ,
,![]() ,
,
由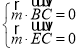 ,得
,得 ,取
,取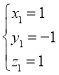 ,则
,则![]() .
.
由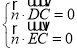 ,得
,得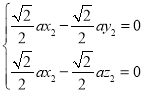 ,取
,取![]() ,则
,则![]() .
.
所以![]() .
.
故平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
解法二:
令![]() ,由已知及(1)可得:
,由已知及(1)可得:![]() ,
,
所以![]() ,
,![]() 均为棱长为a的正三角形.
均为棱长为a的正三角形.
取![]() 中点G,则
中点G,则![]() ,
,![]() ,故
,故![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在![]() 中,
中,![]() ,
,![]() ,
,
由余弦定理可得:![]() ,
,
故平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 为抛物线
为抛物线![]() 上的两点,
上的两点,![]() 与
与![]() 的中点的纵坐标为4,直线
的中点的纵坐标为4,直线![]() 的斜率为
的斜率为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,
,![]() 、
、![]() 为抛物线
为抛物线![]() (除原点外)上的不同两点,直线
(除原点外)上的不同两点,直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且满足
,且满足![]() ,记抛物线
,记抛物线![]() 在
在![]() 、
、![]() 处的切线交于点
处的切线交于点![]() ,若点
,若点![]() 、
、![]() 的中点的纵坐标为8,求点
的中点的纵坐标为8,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天气预报说,在今后的三天中,每一天下雨的概率均为40%,现部门通过设计模拟实验的方法研究三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,其余6个数字表示不下雨:产生了20组随机数:
907 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
则这三天中恰有两天降雨的概率约为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目,大桥建设需要许多桥梁构件。从某企业生产的桥梁构件中抽取![]() 件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间
件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
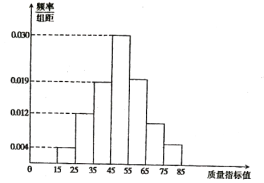
(1)求这些桥梁构件质量指标值落在区间![]() 内的频率;
内的频率;
(2)用分层抽样的方法在区间![]() 内抽取一个容量为
内抽取一个容量为![]() 的样本,将该样本看成一个总体,从中任意抽取
的样本,将该样本看成一个总体,从中任意抽取![]() 件桥梁构件,求这
件桥梁构件,求这![]() 件桥梁构件都在区间
件桥梁构件都在区间![]() 内的概率
内的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】桂林漓江主要景点有象鼻山、伏波山、叠彩山、芦笛岩、七星岩、九马画山,小张一家人随机从这6个景点中选取2个进行游玩,则小张一家人不去七星岩和叠彩山的概率为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】证明:存在无数个满足如下条件的整数組(a,b,c,d):
(1)a>c>0,(a,c)=1;
(2)对任意给定的正整数k,恰有k个正整数n,使得(an+b)|(cn+d)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】作一个平面截正方体![]() 得到一个多边形(包括三角形)截面,那么截面形状可能是__________.(填上所有你认为正确的选项的序号)
得到一个多边形(包括三角形)截面,那么截面形状可能是__________.(填上所有你认为正确的选项的序号)
①正三角形;②正方形;③菱形;④非正方形的矩形;⑤正五边形;⑥正六边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com