Question

建造一个容积为8m³、深为2m的长方体形无盖水池，如果池底和池壁的造价分别为120元/m²和80元/m²．
（1）求总造价y（元）关于底面一边长x（m）的函数解析式；
（2）指出（1）所求函数在区间（0，2）和（2，+∞）上的单调性；并选其中一个给予证明．
（3）说明如何建造使得总造价最少．

Answer 1

分析：（1）底面一边长x，另一边长为

4

x

，底面积为4，侧面积为2×2x+2×

8

x

，所以总造价y可以表示出来；
（2）总造价函数y=（x+

4

x

）×320+480（其中x＞0），用导数法容易证明它在区间（0，2）上单调递减，在区间（2，+∞）上单调递增；
（3）由（2）知，当x=2时，函数y的值最小，即造价最少．

解答：解：（1）设底面一边长x（m），那么令一边长为

4

x

（m），如图：
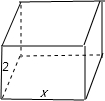
总造价为：y=（2×2x+2×

8

x

）×80+4×120=（x+

4

x

）×320+480（其中x＞0）；
（2）函数y=（x+

4

x

）×320+480（其中x＞0），在区间（0，2）上单调递减，在区间（2，+∞）上单调递增；
现在用导数法证明：∵y^′=320（1-

4

x2

），令y^′=0，则x=±2，只取x=2，∴当0＜x＜2时，y^′＜0，
所以，函数y在区间（0，2）上单调递减，是减函数；
（3）由（2）分析知，当x=2时，函数y的值最小，即当底面边长为2（m）的正方形时，建造的水池造价最少．

点评：本题考查了长方形模型的应用，由长方形的侧面积建立函数解析式，由解析式判断单调性并求最值，是中档题．