练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．若a＞0，b＞0，且a+b=2，则$\frac{1}{a}+\frac{9}{b}$的最小值为8．

    分析 利用“乘1法”与基本不等式的性质即可得出．

    解答 解：∵a＞0，b＞0，且a+b=2，
    则$\frac{1}{a}+\frac{9}{b}$=$\frac{1}{2}（a+b）$$（\frac{1}{a}+\frac{9}{b}）$=$\frac{1}{2}（10+\frac{b}{a}+\frac{9a}{b}）$$≥\frac{1}{2}（10+2\sqrt{\frac{b}{a}•\frac{9a}{b}}）$=$\frac{1}{2}×（10+6）$=8，当且仅当b=3a=$\frac{3}{2}$时取等号．
    故答案为：8．

    点评 本题考查了“乘1法”、基本不等式的性质，考查了分类讨论方法、推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．将函数f（x）=sin2xcos2x+$\sqrt{3}{cos^2}2x-\frac{{\sqrt{3}}}{2}$的图象上所有点纵坐标不变，横坐标伸长到原来的2倍，再向右平行移动$\frac{π}{3}$个单位长度得函数g（x）图象，则以下说法正确的是（　　）
    A．函数g（x）在区间$[{0，\frac{π}{2}}]$上单调递增B．函数f（x）与g（x）的最小正周期均为π
    C．函数g（x）在区间$[{0，\frac{π}{2}}]$上的最大值为$\frac{{\sqrt{3}}}{2}$D．函数g（x）的对称中心为$（{\frac{Kπ}{2}+\frac{π}{6}，0}）$（K∈Z）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

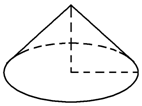    5．如图，某养路处建造圆锥形仓库用于贮藏食盐（供融化高速公路上的积雪之用）．已建的仓库的底面直径为12m，高4m，养路处拟建一个更大的圆锥形仓库，以存放更多的食盐，现有两个方案：一是新建仓库的底面直径比原来的大4m（高不变），二是高度增加4m（底面直径不变）．
    （1）分别计算按这两个方案所建仓库的体积；
    （2）分别计算按这两个方案所建仓库的侧面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．在复平面内，复数$\frac{i}{{\sqrt{3}-3i}}$对应的点位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知x，y满足约束条件$\left\{\begin{array}{l}x+y≤5\\ x-4y≤0\\ x-y+3≥0\end{array}\right.$，则下列目标函数中，在点（4，1）处取得最大值的是（　　）
    A．$z=\frac{1}{5}x-y$B．z=3x+yC．$z=-\frac{1}{5}x-y$D．z=3x-y

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知a∈R，命题$p：\frac{x^2}{2a}+\frac{y^2}{3a-6}=1$表示的曲线是焦点在x轴上的椭圆；命题q：不等式x2+（a+4）x+16＞0的解集为R，若p∧q是真命题，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设函数f（x）=emx+x2-mx．
    （1）讨论f（x）的单调性；
    （2）若对于任意x1，x2∈[-1，1]，都有f（x1）-f（x2）≤e-1，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．设集合M={x|x2-3x+2＞0}，集合$N=\left\{{x|{{（{\frac{1}{2}}）}^x}≥4}\right\}$，则M∩N=（　　）
    A．{x|x＞-2}B．{x|x＜-2}C．{x|x＞-1}D．{x|x≤-2}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．在△ABC中，A、B、C为它的三个内角，设向量$\overrightarrow{p}$=（cos$\frac{B}{2}$，sin$\frac{B}{2}$），$\overrightarrow{q}$=（cos$\frac{B}{2}$，-sin$\frac{B}{2}$），且$\overrightarrow{p}$与$\overrightarrow{q}$的夹角为$\frac{π}{3}$．
    （1）求角B的大小；
    （2）已知tanC=$\frac{\sqrt{3}}{2}$，求$\frac{sin2AcosA-sinA}{sin2Acos2A}$的值．

    查看答案和解析>>

    同步练习册答案