练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在等比数列{an}中，a1＝2，前n项和为Sn ， 若数列{an＋1}也是等比数列，则Sn等于（ ）．
    A.2n＋1－2
    B.3n
    C.2n
    D.3n－1

    【答案】C
    【解析】∵数列{an}为等比数列，设公比为q，∴an＝2qn－1，又∵{an＋1}也是等比数列，则(an＋1＋1)2＝(an＋1)·(an＋2＋1) ＋2an＋1＝anan＋2＋an＋an＋2an＋an＋2＝2an＋1an(1＋q2－2q)＝0q＝1.即an＝2，所以Sn＝2n，故C符合题意.

    所以答案是：C .
    【考点精析】关于本题考查的等比数列的通项公式（及其变式）和等比数列的基本性质，需要了解通项公式：；{an}为等比数列，则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】四棱锥P﹣ABCD中，PB⊥底面ABCD，CD⊥PD．底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3．点E在棱PA上，且PE=2EA． （Ⅰ）求异面直线PA与CD所成的角；
    （Ⅱ）求证：PC∥平面EBD；
    （Ⅲ）求二面角A﹣BE﹣D的大小．（用反三角函数表示）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥P﹣ABCD中PA⊥平面ABCD，且PA=4PQ=4，底面为直角梯形， ∠CDA=∠BAD=90°， ，M，N分别是PD，PB的中点．

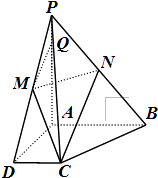
    （1）求证：MQ∥平面PCB；
    （2）求截面MCN与底面ABCD所成二面角的大小；
    （3）求点A到平面MCN的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．求证：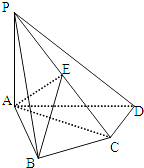

    （Ⅰ）CD⊥AE；
    （Ⅱ）PD⊥平面ABE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用斜二测画法画出图中水平放置的△OAB的直观图．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在 中， ， ，点 在 边上，且 ， ．

    （I）求 ；
    （II）求 的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知x>0,y>0,且2x+8y-xy=0,求:
    （1）xy的最小值;
    （2）x+ y的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题： ①﹣3是函数y=f（x）的极值点；
    ②﹣1是函数y=f（x）的最小值点；
    ③y=f（x）在x=0处切线的斜率小于零；
    ④y=f（x）在区间（﹣3，1）上单调递增．
    则正确命题的序号是 ．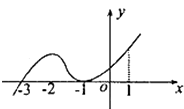

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= 过点（1，e）．
    （1）求y=f（x）的单调区间；
    （2）当x＞0时，求 的最小值；
    （3）试判断方程f（x）﹣mx=0（m∈R且m为常数）的根的个数．

    查看答案和解析>>

    同步练习册答案