
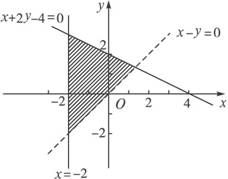
试用关于x、y的不等式组表示图中阴影部分所示的平面区域_______________.
思路点拨:本题要写出对应图形如何用相应的不等式表示出来,只要在对应的平面区域中任取一个点,将其坐标分别代入对应的直线的一般式方程的左边的代数式中去,判断其符号即可写出相应的不等式组.
由所给的图形可以看到,点(-1,0)在相应的平面区域内,把点(-1,0)的坐标分别代入y-x、x+2y-4、y+2中,使得y-x>0,x+2y-4<0,x+2>0,同时注意相应平面的区域是否包括边界在内,故图中阴影部分所示的平面区域用不等式组表示为

答案:
[一通百通]对于二元一次不等式Ax+By+C>0(或Ax+By+C<0)所表示的平面区域问题,在解决过程中只要能够抓住一个特殊点相对于对应直线的位置,并将相应的点的坐标代入Ax+By+C中,注意判断其符号,从而将其所表示的平面区域确定.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 3 |
| π |
| 6 |
| π |
| 4 |

查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省盐城市高二(下)期末数学试卷(文科)(解析版) 题型:解答题
 米,
米, ,AE,EG,HF,FC的造价均为每米1万元,GH的造价为每米2万元,设MN与AB所成的角为α(α∈[0,
,AE,EG,HF,FC的造价均为每米1万元,GH的造价为每米2万元,设MN与AB所成的角为α(α∈[0,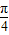 ]),天桥的总造价(由AE,EG,GH,HF,FC五段构成,GM与HN忽略不计)为W万元.
]),天桥的总造价(由AE,EG,GH,HF,FC五段构成,GM与HN忽略不计)为W万元.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省盐城市高二(下)期末数学试卷(理科)(解析版) 题型:解答题
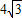 米,
米, ,AE,EG,HF,FC的造价均为每米1万元,GH的造价为每米2万元,设MN与AB所成的角为α(α∈[0,
,AE,EG,HF,FC的造价均为每米1万元,GH的造价为每米2万元,设MN与AB所成的角为α(α∈[0,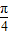 ]),天桥的总造价(由AE,EG,GH,HF,FC五段构成,GM与HN忽略不计)为W万元.
]),天桥的总造价(由AE,EG,GH,HF,FC五段构成,GM与HN忽略不计)为W万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com