
| A. | $\sqrt{2}$ | B. | $±2\sqrt{2}$ | C. | $±\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 当点A在第一象限,通过抛物线定义及AF=2BF可知B为CE中点,通过勾股定理可知AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=2$\sqrt{2}$BC,进而计算可得结论.
解答  解:如图,点A在第一象限.
解:如图,点A在第一象限.
过A、B分别作抛物线的垂线,垂足分别为D、E,
过A作EB的垂线,垂足为C,则四边形ADEC为矩形.
由抛物线定义可知AD=AF,BE=BF,
又∵AF=2BF,
∴AD=CE=2BE,即B为CE中点,
∴AB=3BC,
在Rt△ABC中,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=2$\sqrt{2}$BC,
∴直线l的斜率为$\frac{AC}{BC}$=$2\sqrt{2}$;
当点B在第一象限时,同理可知直线l的斜率为-$2\sqrt{2}$,
∴直线l的斜率为±$2\sqrt{2}$,
故选:B.
点评 本题考查抛物线的简单性质,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
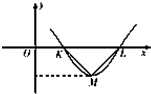 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )| A. | $-\frac{{\sqrt{3}}}{4}$ | B. | $-\frac{1}{4}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com