【题目】下图是某地区2009年至2018年芯片产业投资额
(单位：亿元)的散点图，为了预测该地区2019年的芯片产业投资额，建立了与时间变量
的四个线性回归模型．根据2009年至2018年的数据建立模型①；根据2010年至2017年的数据建立模型②；根据2011年至2016年的数据建立模型③；根据2014年至2018年的数据建立模型④．则预测值更可靠的模型是（ ）
A.①B.②C.③D.④
优等生题库系列答案
53天天练系列答案科目：高中数学 来源： 题型：
【题目】某医院对治疗支气管肺炎的两种方案A，B进行比较研究，将志愿者分为两组，分别采用方案A和方案B进行治疗，统计结果如下：
有效 | 无效 | 合计 | |
使用方案A组 | 96 | 120 | |
使用方案B组 | 72 | ||
合计 | 32 |
(1)完成上述列联表，并比较两种治疗方案有效的频率；
(2)能否在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关？
附：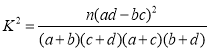
.
P( | 0.005 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，矩形ABCD中，AD＝2AB＝4，E为BC的中点，现将△BAE与△DCE折起，使得平面BAE及平面DEC都与平面ADE垂直．
（1）求证：BC∥平面ADE；
（2）求二面角A﹣BE﹣C的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两位同学参加诗词大会，设甲、乙两人每道题答对的概率分别为
和
.假定甲、乙两位同学答题情况互不影响，且每人各次答题情况相互独立.
（1）用
表示甲同学连续三次答题中答对的次数，求随机变量的分布列和数学期望；
（2）设
为事件“甲、乙两人分别连续答题三次，甲同学答对的次数比乙同学答对的次数恰好多2”，求事件发生的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将4本不同的书随机放入如图所示的编号为1，2，3，4的四个抽屉中.
1 | 2 | 3 | 4 |
（Ⅰ）求4本书恰好放在四个不同抽屉中的概率；
（Ⅱ）随机变量
表示放在2号抽屉中书的本数，求的分布列和数学期望
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】近年来，我国多地区遭遇了雾霾天气，引起口罩热销．某品牌口罩原来每只成本为6元．售价为8元，月销售5万只．
（1）据市场调查，若售价每提高0.5元，月销售量将相应减少0.2万只，要使月总利润不低于原来的月总利润（月总利润
月销售总收入
月总成本），该口罩每只售价最多为多少元？
（2）为提高月总利润，厂家决定下月进行营销策略改革，计划每只售价
元，并投入
万元作为营销策略改革费用．据市场调查，每只售价每提高0.5元，月销售量将相应减少
万只．则当每只售价
为多少时，下月的月总利润最大？并求出下月最大总利润．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】狄利克雷是19世纪德国著名的数学家，他定义了一个“奇怪的函数”
，下列关于狄利克雷函数的叙述正确的有：______.
①
的定义域为
，值域是
②具有奇偶性，且是偶函数
③是周期函数，但它没有最小正周期 ④对任意的
，
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
