
【题目】下列判断正确的是 . (填写所有正确的序号) ①若sinx+siny= ![]() ,则siny﹣cos2x的最大值为
,则siny﹣cos2x的最大值为 ![]() ;
;
②函数y=sin(2x+ ![]() )的单调增区间是[kπ﹣
)的单调增区间是[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z;
],k∈Z;
③函数f(x)= ![]() 是奇函数;
是奇函数;
④函数y=tan ![]() ﹣
﹣ ![]() 的最小正周期是π.
的最小正周期是π.
【答案】④
【解析】解:①若sinx+siny= ![]() ,可得siny=
,可得siny= ![]() ﹣sinx∈[﹣1,1],
﹣sinx∈[﹣1,1],
解得﹣ ![]() ≤sinx≤1,则siny﹣cos2x=
≤sinx≤1,则siny﹣cos2x= ![]() ﹣sinx﹣(1﹣sin2x)=(sinx﹣
﹣sinx﹣(1﹣sin2x)=(sinx﹣ ![]() )2﹣
)2﹣ ![]() ,
,
当sinx=﹣ ![]() 时,取得最大值为
时,取得最大值为 ![]() ,故①错;②由2kπ﹣
,故①错;②由2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,可得kπ﹣
,可得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
函数y=sin(2x+ ![]() )的单调增区间是[kπ﹣
)的单调增区间是[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z,故②错;③函数f(x)=
],k∈Z,故②错;③函数f(x)= ![]() ,可得1+sinx+cosx≠0,即为
,可得1+sinx+cosx≠0,即为 ![]() sin(x+
sin(x+ ![]() )≠﹣1,
)≠﹣1,
即有x+ ![]() ≠2kπ+
≠2kπ+ ![]() 且x+
且x+ ![]() ≠2kπ+
≠2kπ+ ![]() ,即为x≠2kπ+π且x≠2kπ+
,即为x≠2kπ+π且x≠2kπ+ ![]() ,
,
则定义域不关于原点对称,f(x)为非奇非偶函数,故③错;④y=tan ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() ,∴T=π.故④对.
,∴T=π.故④对.
所以答案是:④.
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 2 | ﹣2 | 0 |
(1)请将上表数据补充完整,并直接写出函数f(x)的解析式;
(2)将函数y=f(x)的图象向左平移 ![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一个几何体的三视图及其尺寸(单位:cm),则该几何体的表面积和体积分别为( ) 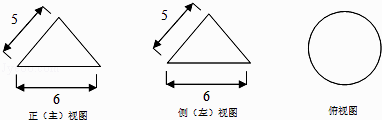
A.24πcm2 , 12πcm3
B.15πcm2 , 12πcm3
C.24πcm2 , 36πcm3
D.15πcm2 , 36πcm3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 ![]() . (Ⅰ)求椭圆C的标准方程;
. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一批产品的长度(单位:mm)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.用频率估计概率,现从该批产品中随机抽取一件,则其为二等品的概率为( ) 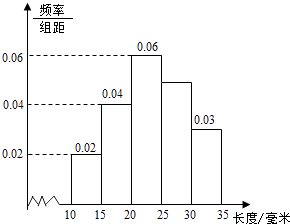
A.0.09
B.0.20
C.0.25
D.0.45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=2,BC= ![]() ,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( )
,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: ①平面A′FG⊥平面ABC;
②BC∥平面A′DE;
③三棱锥A′﹣DEF的体积最大值为 ![]() a3;
a3;
④动点A′在平面ABC上的射影在线段AF上;
⑤二面角A′﹣DE﹣F大小的范围是[0, ![]() ].
].
其中正确的命题是(写出所有正确命题的编号)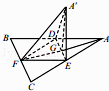
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)的定义域为(﹣a,0)∪(0,a)(0<a<1),其图象上任意一点P(x,y)满足x2+y2=1,则给出以下四个命题:①函数y=f(x)一定是偶函数;②函数y=f(x)可能是奇函数;③函数y=f(x)在(0,a)上单调递增④若函数y=f(x)是偶函数,则其值域为(a2 , 1)其中正确的命题个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面是被严重破坏的频率分布表和频率分布直方图,根据残表和残图,则 p= , q= .
分数段 | 频数 | |
[60,70) | p | |
[70,80) | 90 | |
[80,90) | 60 | |
[90,100] | 20 | q |
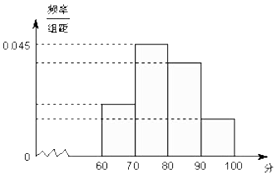
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com