
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ![]() =(1,2)
=(1,2)
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标;
的坐标;
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ.
的夹角θ.
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分为14分)如图1所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4.如图2所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连结AB,设点F是AB的中点.
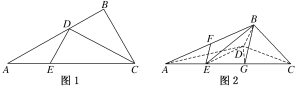
(1)求证:DE⊥平面BCD;
(2)在图2中,若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥BDEG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于三角形满足的条件,下列判断正确的是( )
A.a=7,b=14,A=30°,有两解
B.a=30,b=25,A=150°,有一解
C.a=6,b=9,A=45°,有两解
D.b=9,c=10,B=60°,无解
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+2ax﹣b2+4
(1)若a是从0,1,2三个数中任取的一个数,b是从﹣2,﹣1,0,1,2五个数中任取的一个数,求函数f(x)有零点的概率;
(2)若a是从区间[﹣3,3]上任取的一个数,b是从区间[0,3]上任取的一个数,求函数g(x)=f(x)+5无零点的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x,g(x)=ax+2(a>0),若x1∈[﹣1,2],x2∈[﹣1,2],使得f(x1)=g(x2),则实数a的取值范围是( )
A.![]()
B.![]()
C.(0,3]
D.[3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1 , D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形. 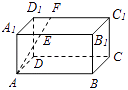
(I)在图中画出这个正方形(不必说明画法和理由);
(II)求直线AF与平面α所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)+1(0≤φ≤ ![]() )的图象相邻两对称轴之间的距离为π,且在x=
)的图象相邻两对称轴之间的距离为π,且在x= ![]() 时取得最大值2.
时取得最大值2.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间;
(3)当f(α)= ![]() ,且
,且 ![]() <α<
<α< ![]() ,求sinα的值.
,求sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x3+3x2﹣mx+1在[﹣2,2]上为单调增函数,则实数m的取值范围为( )
A.m≤﹣3
B.m≤0
C.m≥﹣24
D.m≥﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com