
 和
和 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中: 的分布列与期望.
的分布列与期望.
 有分布列
有分布列 | 0 | 1 | 2 | 3 | 4 |
| P | 1/36 | 1/6 | 13/36 | 1/3 | 1/9 |
 的期望为
的期望为
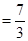 (株)
(株) 表示甲种大树成活k株,k=0,1,2 …………………… 1 分
表示甲种大树成活k株,k=0,1,2 …………………… 1 分 表示乙种大树成活l株,l=0,1,2 ,先计算出
表示乙种大树成活l株,l=0,1,2 ,先计算出 ,它都属于n次独立重复试验发生n次的概率.
,它都属于n次独立重复试验发生n次的概率. .
. 的所有可能值为0,1,2,3,4,然后分别计算出
的所有可能值为0,1,2,3,4,然后分别计算出 取每个值对应的概率,再列出分布列,根据分布列计算出期望值.
取每个值对应的概率,再列出分布列,根据分布列计算出期望值. 表示甲种大树成活k株,k=0,1,2 ……………… 1 分
表示甲种大树成活k株,k=0,1,2 ……………… 1 分 表示乙种大树成活l株,l=0,1,2 …………………… 2分
表示乙种大树成活l株,l=0,1,2 …………………… 2分 ,
, 独立. 由独立重复试验中事件发生的概率公式有
独立. 由独立重复试验中事件发生的概率公式有 ,
, 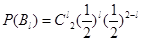 .
. ,
,  ,
,  .…………………… 3 分
.…………………… 3 分 ,
,  ,
, 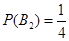 .
. .…………………… 6分
.…………………… 6分 的所有可能值为0,1,2,3,4,且
的所有可能值为0,1,2,3,4,且 ,…………………… 7 分
,…………………… 7 分 ,…………………8 分
,…………………8 分 =
= ……9 分
……9 分 .……… 10 分
.……… 10 分 .……… 11 分
.……… 11 分 有分布列
有分布列 | 0 | 1 | 2 | 3 | 4 |
| P | 1/36 | 1/6 | 13/36 | 1/3 | 1/9 |
 的期望为
的期望为
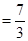 (株)…… 13 分
(株)…… 13 分 分别表示甲乙两种树成活的株数,则
分别表示甲乙两种树成活的株数,则 10分
10分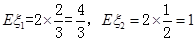 从而知
从而知


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 局者获得这次比赛的胜利,比赛结束.假设在一局比赛中,甲获胜的概率为
局者获得这次比赛的胜利,比赛结束.假设在一局比赛中,甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为 ,各局比赛结果相互独立.现知前
,各局比赛结果相互独立.现知前 局中,甲、乙各胜
局中,甲、乙各胜 局,设
局,设 表示从第
表示从第 局开始到比赛结束所进行的局数,则
局开始到比赛结束所进行的局数,则 的数学期望为 .
的数学期望为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求 的分布列和数学期望
的分布列和数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为 ,且各次投篮互不影响.(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数
,且各次投篮互不影响.(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数 的分布列与期望
的分布列与期望查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
, .
. 的数学期望;
的数学期望;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com