
【题目】如图,在四棱锥PABCD中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP=4,AB=BC=2,M为PC的中点.
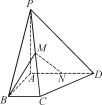
(1)求异面直线AP,BM所成角的余弦值;
(2)点N在线段AD上,且AN=λ,若直线MN与平面PBC所成角的正弦值为![]() ,求λ的值.
,求λ的值.
【答案】(1)![]() .(2)1
.(2)1
【解析】
(1)先根据题意建立空间直角坐标系,求得向量![]() 和向量
和向量![]() 的坐标,再利用线线角的向量方法求解.
的坐标,再利用线线角的向量方法求解.
(2,由AN=λ,设N(0,λ,0)(0≤λ≤4),则![]() =(-1,λ-1,-2),再求得平面PBC的一个法向量,利用直线MN与平面PBC所成角的正弦值为
=(-1,λ-1,-2),再求得平面PBC的一个法向量,利用直线MN与平面PBC所成角的正弦值为![]() ,由|cos〈
,由|cos〈![]() ,
,![]() 〉|=
〉|=![]() =
=![]() =
=![]() 求解.
求解.
(1) 因为PA⊥平面ABCD,且AB,AD平面ABCD,所以PA⊥AB,PA⊥AD.
又因为∠BAD=90°,所以PA,AB,AD两两互相垂直.
分别以AB,AD,AP为x,y,z轴建立空间直角坐标系,
则由AD=2AB=2BC=4,PA=4可得
A(0,0,0),B(2,0,0),C(2,2,0),D(0,4,0),P(0,0,4).
又因为M为PC的中点,所以M(1,1,2).
所以![]() =(-1,1,2),
=(-1,1,2),![]() =(0,0,4),
=(0,0,4),
所以cos〈![]() ,
,![]() 〉=
〉=![]()
=![]() =
=![]() ,
,
所以异面直线AP,BM所成角的余弦值为![]() .
.
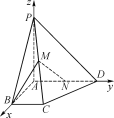
(2) 因为AN=λ,所以N(0,λ,0)(0≤λ≤4),
则![]() =(-1,λ-1,-2),
=(-1,λ-1,-2),![]() =(0,2,0),
=(0,2,0),![]() =(2,0,-4).
=(2,0,-4).
设平面PBC的法向量为![]() =(x,y,z),
=(x,y,z),
则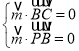 即
即![]()
令x=2,解得y=0,z=1,
所以![]() =(2,0,1)是平面PBC的一个法向量.
=(2,0,1)是平面PBC的一个法向量.
因为直线MN与平面PBC所成角的正弦值为![]() ,
,
所以|cos〈![]() ,
,![]() 〉|=
〉|=![]() =
=![]() =
=![]() ,
,
解得λ=1∈[0,4],
所以λ的值为1.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() ,
,![]() ,
,![]() 的中点.
的中点.
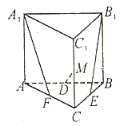
(I)证明:直线![]() 与
与![]() 共面;
共面;
(Ⅱ)证明:平面![]() 平面
平面![]() ;并试写出
;并试写出![]() 到平面
到平面![]() 的距离(不必写出计算过程).
的距离(不必写出计算过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2013年以来,“一带一路”建设成果显著.下图是2013-2017年,我国对“一带一路”沿线国家进出口情况统计图.下列描述错误的是( )
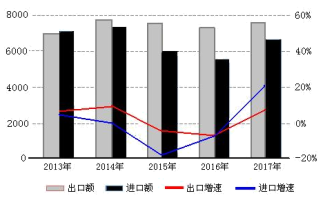
A.这五年,2013年出口额最少
B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降
D.这五年,2017年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
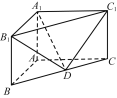
【题目】在直三棱柱ABC-A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中点.
(1) 求直线DC1与平面A1B1D所成角的正弦值;
(2) 求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长AB=3,侧棱AA1=2,E是棱CC1的中点,点F满足![]() =2
=2![]() .
.
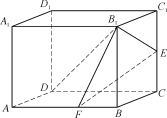
(1)求异面直线FE和DB1所成角的余弦值;
(2)记二面角E-B1F-A的大小为θ,求|cosθ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地实行垃圾分类后,政府决定为![]() 三个小区建造一座垃圾处理站M,集中处理三个小区的湿垃圾.已知
三个小区建造一座垃圾处理站M,集中处理三个小区的湿垃圾.已知![]() 在
在![]() 的正西方向,
的正西方向,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,
方向,![]() 在
在![]() 的北偏西
的北偏西![]() 方向,且在
方向,且在![]() 的北偏西
的北偏西![]() 方向,小区
方向,小区![]() 与
与![]() 相距
相距![]() 与
与![]() 相距
相距![]() .
.
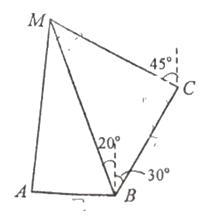
(1)求垃圾处理站![]() 与小区
与小区![]() 之间的距离;
之间的距离;
(2)假设有大、小两种运输车,车在往返各小区、处理站之间都是直线行驶,一辆大车的行车费用为每公里![]() 元,一辆小车的行车费用为每公里
元,一辆小车的行车费用为每公里![]() 元(其中
元(其中![]() 为满足
为满足![]() 是
是![]() 内的正整数) .现有两种运输湿垃圾的方案:
内的正整数) .现有两种运输湿垃圾的方案:
方案1:只用一辆大车运输,从![]() 出发,依次经
出发,依次经![]() 再由
再由![]() 返回到
返回到![]() ;
;
方案2:先用两辆小车分别从![]() 运送到
运送到![]() ,然后并各自返回到
,然后并各自返回到![]() ,一辆大车从
,一辆大车从![]() 直接到
直接到![]() 再返回到
再返回到![]() .试比较哪种方案更合算?请说明理由. 结果精确到小数点后两位
.试比较哪种方案更合算?请说明理由. 结果精确到小数点后两位
查看答案和解析>>
科目:高中数学 来源: 题型:
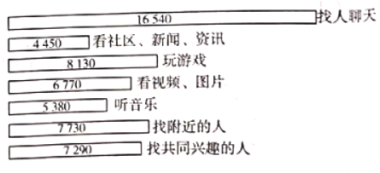
【题目】近年来,随着![]() 网络的普及和智能手机的更新换代,各种方便的
网络的普及和智能手机的更新换代,各种方便的![]() 相继出世,其功能也是五花八门.某大学为了调查在校大学生使用
相继出世,其功能也是五花八门.某大学为了调查在校大学生使用![]() 的主要用途,随机抽取了
的主要用途,随机抽取了![]() 名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
①可以估计使用![]() 主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
②可以估计不足![]() 的大学生使用
的大学生使用![]() 主要玩游戏;
主要玩游戏;
③可以估计使用![]() 主要找人聊天的大学生超过总数的
主要找人聊天的大学生超过总数的![]() .
.
其中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何是美籍法国数学家芒德勃罗在20世纪70年代创立的一门数学新分支,其中的“谢尔宾斯基”图形的作法是:先作一个正三角形,挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的每个小正三角形中又挖去一个“中心三角形”.按上述方法无限连续地作下去直到无穷,最终所得的极限图形称为“谢尔宾斯基”图形(如图所示),按上述操作7次后,“谢尔宾斯基”图形中的小正三角形的个数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】淮北市第一次模拟考试理科共考语文、数学、英语、物理、化学、生物六科,安排在某两日的四个半天考完,每个半天考一科或两科.若语文、数学、物理三科中任何两科不能排在同一个半天,则此次考试不同安排方案的种数有( )(同一半天如果有两科考试不计顺序)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com