练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．已知（x2+2x+1）（1+x）4=a0+a1x+a2x2+…+a7x7，则a1+2a2+3a3+…+7a7=192．

    分析 把题目中的代数式对x两边求导数，再令x=1，即可求出结果．

    解答 解：∵（x2+2x+1）（1+x）4=a0+a1x+a2x2+…+a7x7，
    两边求导数，得：
    （2x+2）（1+x）4+4（1+x）3（x2+2x+1）=a1+2a2x+…+7a7x6，
    令x=1，得（2+2）（1+1）4+4•（1+1）3（12+2+1）=a1+2a2+3a3+…+7a7，
    ∴a1+2a2+3a3+…+7a7=192．
    故答案为：192．

    点评 本题考查了二项式定理的应用问题，也考查了导数的概念与应用问题，考查了特殊值的计算问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    7．已知$\frac{a+b}{c}$=$\frac{b+c}{a}$=$\frac{c+a}{b}$=k，求k的值（提示：要考虑a+b+c=0）的情况．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．复数z满足z（2+i）=3-6i（i为虚数单位），则复数z的虚部为-3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．目前我国很多城市出现了雾霾天气，已经给广大人民的健康带来影响，其中汽车尾气排放是造成雾霾天气的重要因素之一，很多城市提倡绿色出行方式，实施机动车尾号限行．某市为了解民众对“车辆限行”的态度，随机调查了50人，并半调查结果制成如表：
    年龄（岁）[15，25）[25，35）[35，45）[45，55）[55，65）[65，75）
    频数510151055
    赞成人数469634
    （1）若从年龄在[15，25）、[25，35）的被调查者中随机选取2人进行跟踪调查，记选中的4人中不赞成“车辆限行”的人数记为X，求X的分布列和期望；
    （2）把年龄在[15，45）称为中青年，年龄在[45，75）称为中老年，请根据上表完成2×2列联表，并说明民众对“车辆限行”的态度与年龄是否有关联．
    态度
    年龄    		赞成不赞成总计
    中青年
    中老年
    总计
    参考公式和数据：x2=$\frac{n（ad-bc）^{2}}{（a+c）（b+d）（a+b）（c+d）}$
    X2≤2.706＞2.706＞3.841＞6.635
    A、B关联性无关联90%95%99%

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

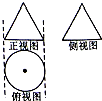    12．一个几何体的三视图如图所示，其中正视图和侧视图都是边长为2的正三角形，那么这个几何体的体积为（　　）
    A．$\frac{\sqrt{3}}{3}π$B．$\frac{\sqrt{2}}{2}π$C．$\frac{\sqrt{2}}{4}π$D．$\frac{π}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

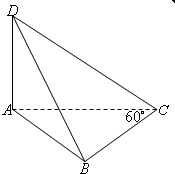    2．如图，四面体D-ABC的体积为$\frac{1}{4}$，且满足∠ACB=60°，BC=1，AD+$\frac{AC}{\sqrt{3}}$=2，则四面体D-ABC中最长棱的长度为（　　）
    A．$\sqrt{3}$B．2C．$\sqrt{5}$D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设l，m是两条不同的直线，α是一个平面，给出以下命题：
    ①若l⊥m，m?α，则l⊥α
    ②若l⊥α，l∥m，则m⊥α
    ③若l∥α，m?α，则l∥m
    ④若l∥α，m∥α，则l∥m．
    其中，正确命题的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．为了解沈阳市高三学生某次模拟考试的数学成绩的某项指标，从所有成绩在及格线以上（90及90分以上）的考生中抽取一部分考生对其成绩进行统计，将成绩按如下方式分成六组，第一组[90，100）、第二组[100，110）…第六组[140，150]．如图为其频率分布直方图的一部分，若第四、五、六组的人数依次成等差数列，且第六组有4人．
    （Ⅰ）请将频率分布直方图补充完整，并估计这组数据的平均数M；
    （Ⅱ）现根据初赛成绩从第四组和第六组中任意选2人，记他们的成绩分别为x，y．若|x-y|≥10，则称此二
    人为“黄金帮扶组”，试求选出的二人为“黄金帮扶组”的概率P1；
    （Ⅲ）用这部分考生成绩分布的频率估计全市考生的成绩分布，并从全市考生中随机抽取三名考生，求成绩不低于120分的人数ξ分布列及期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知a，b，c均为正数，且a+b+c=3，求证：$\frac{{b}^{2}}{a}$+$\frac{{c}^{2}}{b}$+$\frac{{a}^{2}}{c}$≥3．

    查看答案和解析>>

    同步练习册答案