
【题目】已知![]() ,
,![]() 且
且![]() ,向量
,向量![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() .
.
(1)求函数![]() 的解析式,并求当
的解析式,并求当![]() 时,
时,![]() 的单调递增区间;
的单调递增区间;
(2)当![]() ,
,![]() 时,
时,![]() 的最大值为5,求
的最大值为5,求![]() 的值;
的值;
(3)当![]() 时,若不等式
时,若不等式![]() 在
在![]() ,
,![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)f(x)![]() =2asin(2x
=2asin(2x![]() ),单调递增区间为[kπ
),单调递增区间为[kπ![]() ,kπ
,kπ![]() ](k∈Z);(2)a=﹣5或a
](k∈Z);(2)a=﹣5或a![]() .(3)(0,1).
.(3)(0,1).
【解析】
(1)化简f(x)=2asin(2x![]() ),再利用三角函数性质求单调区间;
),再利用三角函数性质求单调区间;
(2)讨论a的正负,确定最大值,求得a;
(3)化简不等式,转化恒成立问题为函数的最值问题,即可求解.
(1)f(x)![]()
![]() 2acos2x
2acos2x![]() asin2x﹣a
asin2x﹣a
=2asin(2x![]() ),
),
∵a>0,
∴2kπ![]() 2x
2x![]() 2kπ
2kπ![]() (k∈Z)
(k∈Z)
∴函数f(x)的单调递增区间为[kπ![]() ,kπ
,kπ![]() ](k∈Z)
](k∈Z)
(2)f(x)=2asin(2x![]() ),
),
当x∈[0,![]() ]时,2x
]时,2x![]() ∈[
∈[![]() ,
,![]() ];
];
若a>0,2a=5,则a![]() ;
;
若a<0,﹣a=5,则a=﹣5;
综上所述,a=﹣5或a![]() .
.
(3)∵|f(x)﹣m|<2在x∈[0,![]() ]上恒成立,
]上恒成立,
∴f(x)﹣2<m<f(x)+2,x∈[0,![]() ]上恒成立,
]上恒成立,
∴f(x)max﹣2<m<f(x)min+2,x∈[0,![]() ]
]
∵f(x)=2sin(2x![]() )在[0,
)在[0,![]() ]上的最大值为2,最小值为﹣1.
]上的最大值为2,最小值为﹣1.
∴0<m<1.
即实数m的取值范围为(0,1).


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】某学习小组在研究性学习中,对昼夜温差大小与绿豆种子一天内出芽数之间的关系进行研究该小组在4月份记录了1日至6日每天昼夜最高、最低温度(如图1),以及浸泡的100颗绿豆种子当天内的出芽数(如图2)

根据上述数据作出散点图,可知绿豆种子出芽数![]() (颗)和温差
(颗)和温差![]() 具有线性相关关系。
具有线性相关关系。
(1)求绿豆种子出芽数![]() (颗)关于温差
(颗)关于温差![]() 的回归方程
的回归方程![]() ;
;
(2)假如4月1日至7日的日温差的平均值为11℃,估计4月7日浸泡的10000颗绿豆种子一天内的出芽数。
附:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.
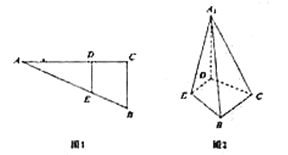
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 长为多少时,异面直线
长为多少时,异面直线![]() ,
,![]() 所成的角最小,并求出此时所成角的余弦值.
所成的角最小,并求出此时所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年100个家庭的月均用水量(单位:t),将数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,制成了如图所示的频率分布直方图.
分成5组,制成了如图所示的频率分布直方图.
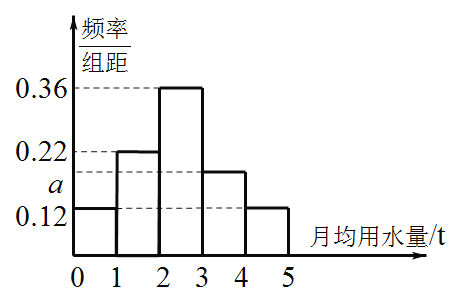
(1)求图中a的值;
(2)设该市有10万个家庭,估计全市月均用水量不低于![]() 的家庭数;
的家庭数;
(3)假设同组中的每个数据都用该组区间的中点值代替,估计全市家庭月均用水量的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解上、下班时期的交通情况,某市抽取了12辆机动车行驶的时速,得到了如下数据(单位:km/h).
上班时期:30 33 18 27 32 40 26 28 21 28 35 20
下班时期:27 19 32 29 36 29 30 22 25 16 17 30
用茎叶图表示这些数据,并分别估计出该市上、下班时期机动车行驶的平均时速.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为了解辖区住户中离退休老人每天的平均户外“活动时间”,从辖区住户的离退休老人中随机抽取了100位老人进行调查,获得了每人每天的平均户外“活动时间”(单位:小时),活动时间按照[0,0.5),[0.5,1),…,[4,4.5]从少到多分成9组,制成样本的频率分布直方图如图所示.

(Ⅰ)求图中a的值;
(Ⅱ)估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数;
(III)在[1.5,2)、[2,2.5)这两组中采用分层抽样抽取9人,再从这9人中随机抽取2人,求抽取的两人恰好都在同一个组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com