解:1.(1)∵z=m(m-1)+(m
2+2m-3)i=0,∴
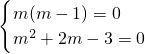
,解得m=1;
(2)∵z=m(m-1)+(m
2+2m-3)i是纯虚数,∴
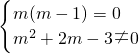
,解得m=0;
(3)∵z=m(m-1)+(m
2+2m-3)i=2+5i,∴
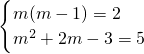
,解得m=2,
2.∵z=m(m-1)+(m
2+2m-3)i,且|z|=1,∴m
2(m-1)
2+(m
2+2m-3)
2=1
化简得,2m
4+2m
3-m
2-12m+8=0 ①,
∵(3+4i)•z=(3+4i)[m(m-1)+(m
2+2m-3)i]=(-m
2-11m+12)+(7m
2+2m-9)i,且它是纯虚数,
∴-m
2-11m+12=0,解得,m=-12或1,代入①式验证也成立,故
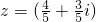
,
则

=
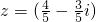
.
分析:1、(1)根据实部和虚部为零,列出方程进行求解;(2)令它的实部为零,虚部不为零列出方程进行求解;
(3)根据实部和虚部对应相等,列出方程进行求解;
2、利题意中复数的模列出一个方程,再由已知的复数是纯复数,由它的实部为零,虚部不为零列出一个方程,组成方程组进行求解,再求出它的共轭复数.
点评:本题考查复数的综合知识的应用,涉及了共轭复数和复数相等的定义、纯虚数的定义的应用,难度不大,主要考查了基本的定义.

 .
.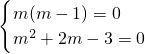 ,解得m=1;
,解得m=1;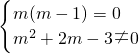 ,解得m=0;
,解得m=0;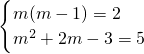 ,解得m=2,
,解得m=2,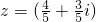 ,
, =
=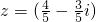 .
.

 学业测评一课一测系列答案
学业测评一课一测系列答案