
【题目】已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与
两点,与![]() 轴,
轴, ![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() ,且
,且![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,
轴的对称点, ![]() 的延长线交椭圆于点
的延长线交椭圆于点![]() ,过点
,过点![]() 分别做
分别做![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() .
.
(1) 若椭圆![]() 的左、右焦点与其短轴的一个端点是正三角形的三个顶点,点
的左、右焦点与其短轴的一个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上,求椭圆
上,求椭圆![]() 的方程;
的方程;
(2)当![]() 时,若点
时,若点![]() 平分线段
平分线段![]() ,求椭圆
,求椭圆![]() 的离心率.
的离心率.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球,再从装有1个蓝球与2个白球的袋中任意摸出1个球,根据摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:
奖级 | 摸出红、蓝球个数 | 获奖金额 |
一等奖 | 3红1蓝 | 200元 |
二等奖 | 3红0蓝 | 50元 |
三等奖 | 2红1蓝 | 10元 |
其余情况无奖且每次摸奖最多只能获得一个奖级.
(1)求一次摸奖恰好摸到1个红球的概率;
(2)求摸奖者在一次摸奖中获奖金额X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上一点,且
上一点,且![]() ,
,![]() .
.
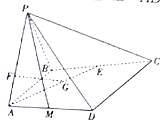
(1)确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)试问:直线![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() ,若存在,求
,若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产 ![]() ,
, ![]() 两种产品,根据市场调查与预测,
两种产品,根据市场调查与预测, ![]() 产品的利润与投资关系如图(1)所示;
产品的利润与投资关系如图(1)所示; ![]() 产品的利润与投资的算术平方根成正比,其关系如图(2)所示(注:利润和投资单位:万元).
产品的利润与投资的算术平方根成正比,其关系如图(2)所示(注:利润和投资单位:万元).
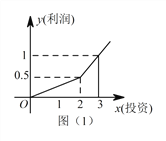
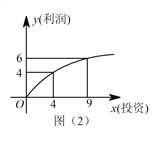
(1)分别将 ![]() ,
, ![]() 两种产品的利润表示为投资的函数关系式;
两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到 ![]() 万元资金,并将全部投入
万元资金,并将全部投入 ![]() ,
, ![]() 两种产品的生产.问怎样分配这
两种产品的生产.问怎样分配这 ![]() 万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中是假命题的是
A. “昆虫都是6条腿,竹节虫是昆虫,所以竹节虫有6条腿”此推理属于演绎推理.
B. “在平面中,对于三条不同的直线![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,
, ![]() 则
则![]() ,将此结论放到空间中也成立” 此推理属于合情推理.
,将此结论放到空间中也成立” 此推理属于合情推理.
C. “![]() ”是“函数
”是“函数![]()
![]() 存在极值”的必要不充分条件.
存在极值”的必要不充分条件.
D. 若![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com