

思路解析:根据判定定理,要证线面垂直,需证直线和平面内的两条直线垂直.根据H是△ABC的垂心,可知BC⊥AH,又PA、PB、PC两两垂直,得PA⊥面PBC,于是PA⊥BC,BC垂直于平面PAH内的相交直线PA和AH.
证明:∵H是△ABC的垂心,
∴AH⊥BC. ①
∵PA⊥PB,PB⊥PC,PB∩PC=P,
∴PA⊥平面PBC.
又∵BC 平面PBC,PA⊥BC, ②
平面PBC,PA⊥BC, ②
由①②知,BC⊥平面PAH,从而BC⊥PH,
同理,AB⊥PH,
∴PH⊥平面ABC.
方法归纳 根据所求证的结论寻求所需的已知条件,看题目是否已经直接给出,或者从题目所给条件经过推理能够得出,这是分析问题的重要方法,称为执果索因;也可从条件出发,将这一条件可能得出的结论一一列出,从中筛选出我们证题所需要的结论,这种分析问题的方法称为由因导果,它发散性较强.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
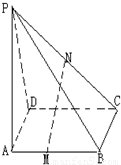
 如图,已知P是平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点.
如图,已知P是平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点.| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省杭州市建德市新安江中学高二(上)期中数学试卷(文科)(解析版) 题型:解答题
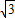 ,求异面直线PA与MN所成的角的大小.
,求异面直线PA与MN所成的角的大小.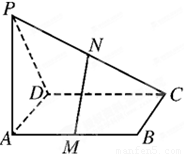
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山西省大同实验中学高二(上)第一次月考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山西省大同实验中学高二(上)第一次月考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com