
如图,已知
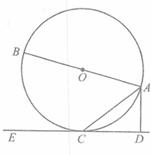
AB是⊙O的直径,C为圆上任意一点,过C的切线分别与过A、B两点的切线交于P、Q.求证:
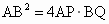 .
.

|
证法 1:连结OP、OQ,如图.∵AP、PQ、BQ为⊙O的切线,∴∠1=∠2 ,∠3=∠4.∵AP 、BQ为⊙O切线,AB为直径,∴AB⊥AP,AB⊥BQ.∴AP∥BQ.∴∠A=∠B=90 °,∠1+∠2+∠3+∠4=180°.∴∠1+∠4=∠2+∠3=90°.∵∠1 +∠5=90°,∴∠4=∠5.∴△AOP∽△BQO.∴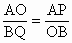 . .
∵AB=2AO=2OB ,∴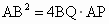 . .
证法 2:连结OC.同上可证得∠2+∠3=90°.∵PQ 切⊙O于C点,∴OC⊥PQ.在 Rt△PQO中,由射影定理可得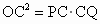 , ,
利用切线长定理,有 PC=AP,BQ=QC.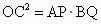 , ,
∵AB=2OC ,∴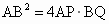 . .
证法 3:如图,过P作BQ的垂线PD,垂足为D.
∵AP 、BQ、PQ切⊙O于A、B、C,∴∠A=∠B=90°,AP=PC,CQ=BQ.∴ 四边形ABDP为矩形,PQ=AB+BQ.∴AP=BD,AB=PD.在 Rt△PQD中,利用勾股定理得: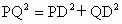 , ,
∴ ∴ |
|
分析:本题利用切线长定理以及相似三角形或勾股定理等,证法较多.
|


科目:高中数学 来源: 题型:
 选做题
选做题查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.
如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
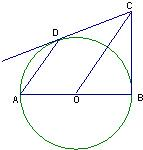 如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD,OA=2.
如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD,OA=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com