
分析 (Ⅰ)设M(x,y),由已知得B(x,-3),A(0,-1)并代入$\overrightarrow{MA}•\overrightarrow{AB}=\overrightarrow{MB}•\overrightarrow{BA}$,$\overrightarrow{MB}$∥$\overrightarrow{OA}$,即可求得M点的轨迹C的方程;
(Ⅱ)设P(x0,y0)为C上的点,求导,写出C在P点处的切线方程,利用点到直线的距离公式即可求得O点到l距离,然后利用基本不等式求出其最小值.
解答 解:(Ⅰ)设点M(x,y),∵$\overrightarrow{MB}$∥$\overrightarrow{OA}$,∴B(x,-3),
∴$\overrightarrow{MA}=(-x,-1-y)$,$\overrightarrow{MB}=(0,-3-y)$,$\overrightarrow{AB}=(x,-2)$,
∴$\overrightarrow{MA}+\overrightarrow{MB}=(-x,-4-2y)$,
∵$\overrightarrow{MA}•\overrightarrow{AB}=\overrightarrow{MB}•\overrightarrow{BA}$,
∴$\overrightarrow{MA}•\overrightarrow{AB}-\overrightarrow{MB}•\overrightarrow{BA}$=$\overrightarrow{MA}•\overrightarrow{AB}+\overrightarrow{MB}•\overrightarrow{AB}$
=($\overrightarrow{MA}$+$\overrightarrow{MB}$)•$\overrightarrow{AB}$=0,
∴(-x,-4-2y)•(x,-2)=0,
即为-x2+2(4+2y)=0,即有$y=\frac{1}{4}{x^2}-2$,
∴曲线C的方程 $y=\frac{1}{4}{x^2}-2$;
(Ⅱ)设P(x0,y0),∵$y=\frac{1}{4}{x^2}-2$,
∴${y^/}=\frac{1}{2}x$,$k=\frac{1}{2}{x_0}$,
∴l:$y-{y_0}=\frac{1}{2}{x_0}(x-{x_0})$,即${x_0}x-2y+2{y_0}-x_0^2=0$,
∴O到直线l的距离$d=\frac{{|2{y_0}-{x_0}^2|}}{{\sqrt{{x_0}^2+4}}}$=$\frac{{\frac{1}{2}{x_0}^2+4}}{{\sqrt{{x_0}^2+4}}}$=$\frac{1}{2}(\frac{4}{{\sqrt{{x_0}^2+4}}}+\sqrt{x_0^2+4})$,
∵$\frac{4}{{\sqrt{{x_0}^2+4}}}+\sqrt{x_0^2+4}≥4$,d≥2,
∴当且仅当x0=0时,dmin=2.
点评 此题是个中档题.考查向量与解析几何的交汇点命题及代入法求轨迹方程,以及导数的几何意义和点到直线的距离公式,综合性强,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
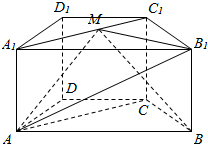 在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1.
在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
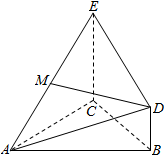 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE且CE=CA=2BD,M是EA的中点.
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE且CE=CA=2BD,M是EA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
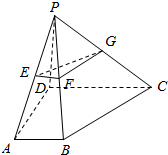 如图,四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}AD$=1.
如图,四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}AD$=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com