
【题目】已知抛物线![]() (
(![]() ),焦点
),焦点![]() 到准线的距离为
到准线的距离为![]() ,过点
,过点![]()
![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于点
于点![]() (点
(点![]() 在第一象限).
在第一象限).
(Ⅰ)若点![]() 焦点
焦点![]() 重合,且弦长
重合,且弦长![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)若点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 交x轴于点
交x轴于点![]() ,且
,且![]() ,求证:点B的坐标是
,求证:点B的坐标是![]() ,并求点
,并求点![]() 到直线
到直线![]() 的距离
的距离![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) ![]() 或
或![]() .(Ⅱ)
.(Ⅱ) 
【解析】
试题分析:(Ⅰ)确定抛物线的方程,设出直线方程与抛物线方程联立,利用弦长|PQ|=2,即可求直线l的方程;(Ⅱ)设出直线方程与抛物线方程联立,利用韦达定理,结合向量知识,证明B(-![]() ,0),确定出
,0),确定出![]() ,或m的范围,表示出点B到直线l的距离d,即可求得取值范围
,或m的范围,表示出点B到直线l的距离d,即可求得取值范围
试题解析:(Ⅰ)解:由题意可知,![]() ,故抛物线方程为
,故抛物线方程为![]() ,焦点
,焦点![]() .
.
设直线l的方程为![]() ,
,![]()
![]() ,
,![]() .
.
由 消去x,得
消去x,得![]() .所以△=n2+1>0,
.所以△=n2+1>0,![]() .
.
因为![]() ,点A与焦点F重合,
,点A与焦点F重合,
所以![]() .
.
所以n2=1,即n=±1.所以直线l的方程为![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
(Ⅱ)证明:设直线l的方程为![]() (m≠0),
(m≠0),![]() ,
,![]() 则
则![]()
由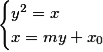 消去x,得
消去x,得![]() ,
,
因为![]() ,所以△=m2+4x0>0,y1+y2=m,y1y2=-x0.
,所以△=m2+4x0>0,y1+y2=m,y1y2=-x0.
设B(xB,0),则![]() .
.
由题意知,![]() ,所以
,所以![]() ,
,
即![]() .
.
显然![]() ,所以
,所以![]() ,即证B(-x0,0).
,即证B(-x0,0).
由题意知,△MBQ为等腰直角三角形,所以![]() ,即
,即![]() ,也即
,也即![]() ,
,
所以![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() >0,即
>0,即![]()
又因为![]() ,所以
,所以![]() .
.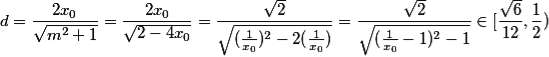 ,
,
所以d的取值范围是 .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() ,定点
,定点![]() ,
, ![]() 是圆
是圆![]() 上的一动点,线段
上的一动点,线段![]() 的垂直平分线交半径
的垂直平分线交半径![]() 于
于![]() 点.
点.
(Ⅰ)求![]() 点的轨迹
点的轨迹![]() 的方程;
的方程;
(Ⅱ)四边形![]() 的四个顶点都在曲线
的四个顶点都在曲线![]() 上,且对角线
上,且对角线![]() ,
, ![]() 过原点
过原点![]() ,若
,若![]() ,求证:四边形
,求证:四边形![]() 的面积为定值,并求出此定值.
的面积为定值,并求出此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用下图的两条线段表示;该商品在30天内日销售量Q(件)与时间t(天)之间的关系Q=﹣t+40. 
(1)根据提供的图象,写出该商品每件的销售价格P与时间t的函数关系式;
(2)问这30天内,哪天的销售额最大,最大是多少?(销售额=销售价格×销售量)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连掷一枚均匀的骰子两次,所得向上的点数分别为![]() ,记
,记![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 事件“![]() ”的概率为
”的概率为![]() B. 事件“
B. 事件“![]() 是奇数”与“
是奇数”与“![]() ”互为对立事件
”互为对立事件
C. 事件“![]() ”与“
”与“![]() ”互为互斥事件 D. 事件“
”互为互斥事件 D. 事件“![]() ”的概率为
”的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一系列函数的解析式和值域相同,但是定义域不同,则称这些函数为“同族函数”,例如函数y=x2 , x∈[1,2],与函数y=x2 , x∈[﹣2,﹣1]即为“同族函数”.下面的函数解析式也能够被用来构造“同族函数”的是( )
A.y=x
B.y=|x﹣3|
C.y=2x
D.y=log ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】销售甲、乙两种商品所得利润分别是P(万元)和Q(万元),它们与投入资金t(万元)的关系有经验公式P=3 ![]() ,Q=t.今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资x(万元).求:
,Q=t.今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资x(万元).求:
(1)经营甲、乙两种商品的总利润y(万元)关于x的函数表达式;
(2)怎样将资金分配给甲、乙两种商品,能使得总利润y达到最大值,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|(x﹣a)[x﹣(a+3)]≤0}(a∈R),B={x|x2﹣4x﹣5>0}.
(1)若A∩B=,求实数a的取值范围;
(2)若A∪B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各式中,正确的个数是( )
①={0};②{0};③∈{0};④0={0};⑤0∈{0};⑥{1}∈{1,2,3};⑦{1,2}{1,2,3};⑧{a,b}={b,a}.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(Ⅰ)求应从小学、中学、大学中分别抽取的学校数目;
(Ⅱ)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com