
已知函数 ,
, 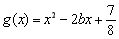 .
.
(Ⅰ)当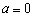 时,求曲线
时,求曲线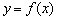 在点
在点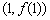 处的切线方程;
处的切线方程;
(Ⅱ)当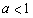 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅲ)当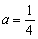 时,函数
时,函数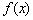 在
在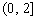 上的最大值为
上的最大值为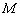 ,若存在
,若存在 ,使得
,使得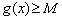 成立,求实数b的取值范围.
成立,求实数b的取值范围.
(Ⅰ)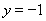 (Ⅱ)当
(Ⅱ)当 时,递增区间为
时,递增区间为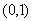 ,
,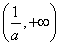 ,递减区间为
,递减区间为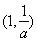
当 时,函数
时,函数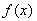 的递增区间为
的递增区间为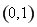 ,递减区间为
,递减区间为
【解析】(Ⅰ)当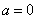 时,
时,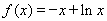
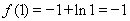 ……………………1分
……………………1分
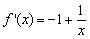
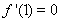 …………………………………….…2分
…………………………………….…2分
所以曲线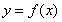 在点
在点 处的切线方程
处的切线方程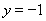 …………………………….…3分
…………………………….…3分
(Ⅱ)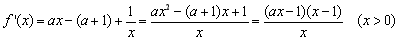 ………4分
………4分
当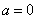 时,
时,
解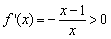 ,得
,得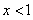 ,解
,解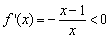 ,得
,得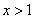
所以函数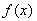 的递增区间为
的递增区间为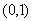 ,递减区间为在
,递减区间为在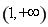 ………………………5分
………………………5分
x | |
|
|
|
| |||||
f’(x) | + |
| - |
| + | |||||
f(x) | 增 |
| 减 |
| 增 | |||||
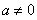 时,令
时,令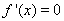 得
得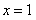 或
或
当 时,
时,
函数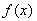 的递增区间为
的递增区间为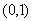 ,
,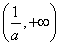 ,递减区间为
,递减区间为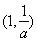 ……………………7分
……………………7分
当 时,
时,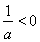 在
在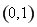 上
上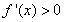 ,在
,在 上
上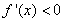 8分
8分
函数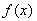 的递增区间为
的递增区间为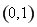 ,递减区间为
,递减区间为 ………………………9分
………………………9分
(Ⅲ)由(Ⅱ)知,当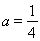 时,
时, 在
在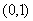 上是增函数,在
上是增函数,在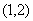 上是减函数,
上是减函数,
所以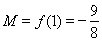 , ……………………………11分
, ……………………………11分
存在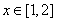 ,使
,使 即存在
即存在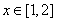 ,使
,使 ,
,
方法一:只需函数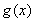 在[1,2]上的最大值大于等于
在[1,2]上的最大值大于等于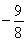
所以有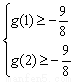 即
即 解得:
解得: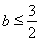 …13分
…13分
方法二:将
整理得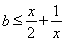
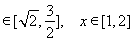 从而有
从而有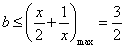
所以 的取值范围是
的取值范围是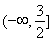 .………13分
.………13分


 口算能手系列答案
口算能手系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十七选修4-4第一节练习卷(解析版) 题型:解答题
从原点O引直线交直线2x+4y-1=0于点M,P为OM上一点,已知OP·OM=1,求P点所在曲线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:选择题
设随机变量X服从正态分布N(0,1),若P(X>1)=p,则P(-1<X<0)=( )
(A)p (B)1-2p
(C) -p (D)p-
-p (D)p-
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数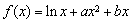 (其中
(其中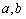 为常数且
为常数且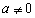 )在
)在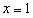 处取得极值.
处取得极值.
(I) 当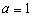 时,求
时,求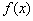 的单调区间;
的单调区间;
(II) 若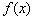 在
在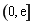 上的最大值为
上的最大值为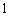 ,求
,求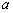 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数 ,
,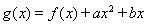 ,函数
,函数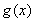 的图象在点
的图象在点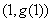 处的切线平行于
处的切线平行于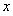 轴.
轴.
(1)确定 与
与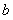 的关系;
的关系;
(2)试讨论函数 的单调性;
的单调性;
(3)证明:对任意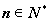 ,都有
,都有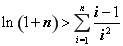 成立。
成立。
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:解答题
已知函数 ,
, ,其中
,其中 的函数图象在点
的函数图象在点 处的切线平行于
处的切线平行于 轴.
轴.
(1)确定 与
与 的关系; (2)若
的关系; (2)若 ,试讨论函数
,试讨论函数 的单调性;
的单调性;
(3)设斜率为 的直线与函数
的直线与函数 的图象交于两点
的图象交于两点 (
( )证明:
)证明: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com