
 (m>0),l1与函数y=|log2x|的图象从左至右相交于点A,B,l2 与函数y=|log2x|的图象从左至右相交于点C,D.记线段AC和BD在X轴上的投影长度分别为a,b,当m变化时,
(m>0),l1与函数y=|log2x|的图象从左至右相交于点A,B,l2 与函数y=|log2x|的图象从左至右相交于点C,D.记线段AC和BD在X轴上的投影长度分别为a,b,当m变化时, 的最小值为( )
的最小值为( )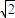



 的最小值.
的最小值. ,log2xD=
,log2xD=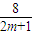 ;
; ,xD=
,xD= .
. =
= =|
=| |=2m•
|=2m• =
= .
. =
= (2m+1)+
(2m+1)+ -
- ≥2
≥2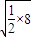 -
- =
= (当且仅当m=
(当且仅当m= 时取“=”)
时取“=”) ≥
≥ =8
=8 .
. =
= 是关键,考查转化与数形结合的思想,考查分析与运算能力,属于难题.
是关键,考查转化与数形结合的思想,考查分析与运算能力,属于难题. 

科目:高中数学 来源: 题型:
| π |
| 12 |
| A、(0,1) | ||||||
B、(
| ||||||
C、(
| ||||||
D、(1,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 8 |
| 2m+1 |
| b |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 8 |
| 2m+1 |
| b |
| a |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、l1与l2一定相交 | B、l1与l2一定平行 | C、l1与l2一定相交或平行 | D、以上说法都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com