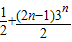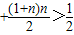【答案】
分析:(1)由函数f(x)是增函数,利用导数得m≥3x
2对任意x∈(0,1)恒成立,从而求出m的范围,即求出集合A;
(2)由(1)中的m的最小值为3,得到f′(x),从而将
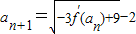
变形得到数列{a
n-1}是首项为2,公比为3的等比数列,即可求数列{a
n}的通项公式;
(3)由(2)可求b
n=na
n=2n•3
n-1+nS
n=2(1•3
+2•3
1+3•3
2+…+n•3
n-1)+(1+2+3+…+n),再利用错位相减法化简得到S
n=
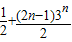
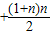
,显然

.
解答:解:(1)f′(x)=-3x
2+m≥0对任意x∈(0,1)恒成立,
所以:m≥3x
2对任意x∈(0,1)恒成立,得m≥3即A=[3,+∞)
(2)由m=3得:f(x)=-x
3+3x⇒f′(x)=-3x
2+3
所以:
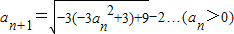
得:a
n+1-1=3(a
n-1)所以数列{a
n-1}是首项为2,公比为3的等比数列
所以:a
n-1=2•3
n-1⇒a
n=2•3
n-1+1
(3)b
n=na
n=2n•3
n-1+nS
n=2(1•3
+2•3
1+3•3
2+…+n•3
n-1)+(1+2+3+…+n)
令:T
n=1•3
+2•3
1+3•3
2+…+n•3
n-13 T
n=1•3
1+2•3
2+…+(n-1)•3
n-1+n•3
n-2 T
n=3
+3
1+3
2+…+3
n-1-n•3
n=
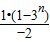
-n•3
n=
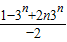
所以T
n=
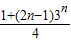
S
n=
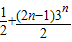
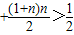 点评:
点评:此题考查导数的应用及数列求和常用的方法--错位相减法.

 ,求数列{an}的通项公式
,求数列{an}的通项公式 .
.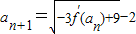 变形得到数列{an-1}是首项为2,公比为3的等比数列,即可求数列{an}的通项公式;
变形得到数列{an-1}是首项为2,公比为3的等比数列,即可求数列{an}的通项公式;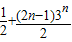
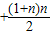 ,显然
,显然 .
.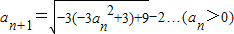
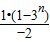 -n•3n=
-n•3n=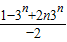
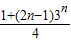 Sn=
Sn=