
分析 (1)利用函数单调性的定义来证明函数的单调性;
(2)根据函数的单调性来求函数在给定区间上的最值问题.
解答 解:(1)f(x)在(-1,+∞)上为增函数,证明如下:
任取-1<x1<x2,则f(x1)-f(x2)=$\frac{2{x}_{1}+1}{{x}_{1}+1}$-$\frac{2{x}_{2}+1}{{x}_{2}+1}$=$\frac{{x}_{1}-{x}_{2}}{({x}_{1}+1)({x}_{2}+1)}$;
∵-1<x1<x2⇒x1+1>0,x2+1>0,x1-x2<0;
∴f(x1)-f(x2)<0⇒f(x1)<f(x2);
所以,f(x)在(-1,+∞)上为增函数.
(2):由(1)知 f(x)[2,4]上单调递增,
∴f(x)的最小值为f(2)=$\frac{2×2+1}{2+1}$=$\frac{5}{3}$,
最大值f(4)=$\frac{2×4+1}{4+1}$=$\frac{9}{5}$.
点评 本题主要考查了函数单调性的定义、函数的最值问题,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | b<c<a | C. | b<a<c | D. | a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
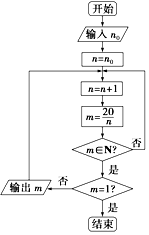 请认真阅读下列程序框图,然后回答问题,其中n0∈N.
请认真阅读下列程序框图,然后回答问题,其中n0∈N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${log_{\frac{1}{3}}}5$ | B. | 5 | C. | -5 | D. | ${({\frac{1}{3}})^5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | $2\sqrt{2}$ | D. | 与m有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{3}$ | B. | -$\frac{7}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com