【题目】已知公差不为零的等差数列{an}中， S2＝16，且
成等比数列.
（1）求数列{an}的通项公式；
（2）求数列{|an|}的前n项和Tn.
【答案】（1）an＝11－2n(n∈N*)．（2）见解析．
【解析】
(1)S2＝16，
成等比数列，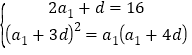
解得首项和公差进而得到通项；（2）当n≤5时，Tn＝a1＋a2＋…＋an, 直接按照等差数列求和公式求和即可, n≥6,Tn＝a1＋a2＋…＋a5－a6－a7－ …－an =n2－10n＋50,写成分段即可.
（1）由S2＝16，成等比数列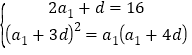，得解得
所以等差数列{an}的通项公式为an＝11－2n(n∈N*)．
（2）当n≤5时，Tn＝|a1|＋|a2|＋…＋|an|＝a1＋a2＋…＋an＝Sn＝－n2＋10n.
当n≥6时，Tn＝|a1|＋|a2|＋…＋|an|＝a1＋a2＋…＋a5－a6－a7－ …－an＝2S5－Sn＝2×(－52＋10×5)－(－n2＋10n)＝n2－10n＋50，
故Tn＝
轻松课堂单元期中期末专题冲刺100分系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
（a＞0，且a≠1）在R上单调递减，且关于x的方程|f（x）|=2﹣x恰好有两个不相等的实数解，则a的取值范围是（ ）
A.（0， 
]
B.[ ， 
]
C.[ 
， ]∪{ }
D.[ ， ）∪{ }
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数f（x）=sin（2x+φ）（|φ|＜π）的图象向左平移 
个单位后关于原点对称，则函数f（x）在[0， 
]上的最小值为（ ）
A.﹣ 
B.﹣ 
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在外接圆直径为1的△ABC中，角A，B，C的对边分别为a，b，c，设向量 
=（a，cosB）， 
=（b，cosA），且 ∥ ， ≠ ．
（1）求sinA+sinB的取值范围；
（2）若abx=a+b，试确定实数x的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分12分） 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表（假设该区域空气质量指数不会超过
）：
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
|
|
|
|
该社团将该校区在
年
天的空气质量指数监测数据作为样本，绘制的频率分布直方图如下图，把该直方图所得频率估计为概率．
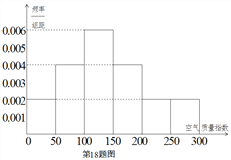
（Ⅰ）请估算
年（以
天计算）全年空气质量优良的天数(未满一天按一天计算)；
（Ⅱ）该校
年
月
、
日将作为高考考场，若这两天中某天出现
级重度污染，需要净化空气费用
元，出现
级严重污染，需要净化空气费用
元，记这两天净化空气总费用为
元，求
的分布列及数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
， 
，在
处的切线方程为
.
（1）求
， 
；
（2）若
，证明： 
.
【答案】（1）
， 
；（2）见解析
【解析】试题分析：（1）求出函数的导数，得到关于
的方程组，解出即可；
（2）由（1）可知
， 
，
由
，可得
，令
， 利用导数研究其单调性可得
，
从而证明
.
试题解析：（（1）由题意
，所以
，
又
，所以
，
若
，则
，与
矛盾，故
， 
.
（2）由（1）可知
， 
，
由
，可得
，
令
，
，
令
当
时， 
， 
单调递减，且
；
当
时， 
， 
单调递增；且
，
所以
在
上当单调递减，在
上单调递增，且
，
故
，
故
.
【点睛】本题考查利用函数的切线求参数的方法，以及利用导数证明不等式的方法，解题时要认真审题，注意导数性质的合理运用.
【题型】解答题
【结束】
22
【题目】在平面直角坐标系
中，曲线
的参数方程为
（
， 
为参数），以坐标原点
为极点， 
轴正半轴为极轴建立极坐标系，直线
的极坐标方程为
，若直线
与曲线
相切；
（1）求曲线
的极坐标方程；
（2）在曲线
上取两点
， 
与原点
构成
，且满足
，求面积
的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数列
中，
在直线
．
（1）求数列{an}的通项公式；
（2）令
，数列
的前n项和为
．
（ⅰ）求；
（ⅱ）是否存在整数λ
，使得不等式(－1)nλ＜
(n∈N
)恒成立？若存在，求出λ的取值的集合；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
