
【题目】已知椭圆![]() 上的一动点
上的一动点![]() 到右焦点的最短距离为
到右焦点的最短距离为![]() ,且右焦点到右准线的距离等于短半轴的长.
,且右焦点到右准线的距离等于短半轴的长.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的任意两个不同的点,连接
轴对称的任意两个不同的点,连接![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,证明直线
,证明直线![]() 与
与![]() 轴相交于定点
轴相交于定点![]() ;
;
(3)在(2)的条件下,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)利用椭圆的定义和性质即可解出a、b、c;(2)利用点斜式方程得出直线PB的方程,与椭圆的方程联立,利用根与系数之间的关系得出点P、B的坐标之间的关系,再利用点斜式表示直线AE的方程,进而即可证明过定点;(3)分类讨论直线MN是否与x轴垂直,与椭圆方程联立得出点MN的坐标之间的关系,再表示出![]() ,进而即可求出其取值范围.
,进而即可求出其取值范围.
(1)由题意可得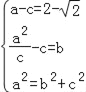 解得
解得![]() ,
,
∴椭圆C的方程为![]() .
.
(2)如图所示:
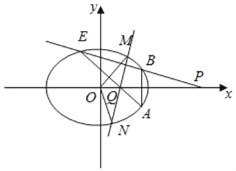
设直线PB的方程为y=k(x﹣4),B(x1,y1),E(x2,y2),
则A(x1,﹣y1).
联立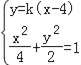 ,消去y化为方程(1+2k2)x2﹣16k2x+32k2﹣4=0,
,消去y化为方程(1+2k2)x2﹣16k2x+32k2﹣4=0,
∵直线PB与椭圆有两个不同的交点,∴△=(16k2)2﹣4(1+2k2)(32k2﹣4)>0.(*)
x1+x2=![]() ,
,![]() .
.
直线AE的方程为![]() ,
,
令y=0,则![]() =
=![]() =
=![]() =
=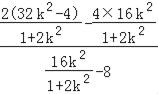 =
=![]() .故直线AE过定点Q(1,0).
.故直线AE过定点Q(1,0).
(3)①当直线MN与x轴重合时,![]() =(2,0)(﹣2,0)=﹣4;
=(2,0)(﹣2,0)=﹣4;
②当直线MN与x轴不重合时,设直线MN的方程为my=x﹣1,
联立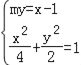 消去x化为方程(2+m2)y2+2my﹣3=0,可知△>0.
消去x化为方程(2+m2)y2+2my﹣3=0,可知△>0.
可得yM+yN=![]() ,yMyN=
,yMyN=![]() .
.
∴![]() =xMxN+yMyN=(myM+1)(myN+1)+yMyN=(1+m2)yMyN+m(yM+yN)+1
=xMxN+yMyN=(myM+1)(myN+1)+yMyN=(1+m2)yMyN+m(yM+yN)+1
=![]() =﹣4+
=﹣4+![]() ,
,
∵m2≥0,∴![]() ,∴
,∴![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.
综上可知:![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如果直线y=kx+1与圆x2+y2+kx+my﹣4=0交于M、N两点,且M、N关于直线x+y=0对称,则不等式组: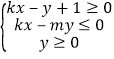 表示的平面区域的面积是( )
表示的平面区域的面积是( )
A.![]()
B.![]()
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 命题“若x2-4x+3=0,则x=3”的逆否命题是:“若x≠3,则x2-4x+3≠0”
B. “x>1”是“|x|>0”的充分不必要条件
C. 若p且q为假命题,则p、q均为假命题
D. 命题p:“x0∈R使得![]() +x0+1<0”,则
+x0+1<0”,则![]() p:“x∈R,均有x2+x+1≥0”
p:“x∈R,均有x2+x+1≥0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等比数列,前n项和为Sn(n∈N*),且 ![]() ﹣
﹣ ![]() =
= ![]() ,S6=63.
,S6=63.
(1)求{an}的通项公式;
(2)若对任意的n∈N* , bn是log2an和log2an+1的等差中项,求数列{(﹣1)n bn2}的前2n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=2 ![]() sin(π﹣x)sinx﹣(sinx﹣cosx)2 .
sin(π﹣x)sinx﹣(sinx﹣cosx)2 .
(1)求f(x)的单调递增区间;
(2)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移 ![]() 个单位,得到函数y=g(x)的图象,求g(
个单位,得到函数y=g(x)的图象,求g( ![]() )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com