
ΓΨΧβΡΩΓΩΡ≥–ΘΈΣΝΥΫβΗΏ“Μ―ß…ζ÷ήΡ©ΒΡΓΑ‘ΡΕΝ ±ΦδΓ±Θ§¥”ΗΏ“ΜΡξΦΕ÷–ΥφΜζ≥ι»ΓΝΥ![]() Οϊ―ß…ζΫχ––Βς•ΥΘ§ΜώΒΟΝΥΟΩ»ΥΒΡ÷ήΡ©ΓΑ‘ΡΕΝ ±ΦδΓ±Θ®ΒΞΈΜΘΚ–Γ ±Θ©Θ§Α¥’’
Οϊ―ß…ζΫχ––Βς•ΥΘ§ΜώΒΟΝΥΟΩ»ΥΒΡ÷ήΡ©ΓΑ‘ΡΕΝ ±ΦδΓ±Θ®ΒΞΈΜΘΚ–Γ ±Θ©Θ§Α¥’’![]() Ζ÷≥…
Ζ÷≥…![]() ΉιΘ§÷Τ≥…―υ±ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γΆΦΥυ ΨΘΚ
ΉιΘ§÷Τ≥…―υ±ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γΆΦΥυ ΨΘΚ
Θ®ΔώΘ©«σΆΦ÷–![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®ΔρΘ©ΙάΦΤΗΟ–ΘΗΏ“Μ―ß…ζ÷ήΡ©ΓΑ‘ΡΕΝ ±ΦδΓ±ΒΡ÷–ΈΜ ΐΘΜ
Θ®ΔσΘ©”Ο―υ±ΨΤΒ¬ ¥ζΧφΗ≈¬ . œ÷¥”»Ϊ–ΘΗΏ“ΜΡξΦΕΥφΜζ≥ι»Γ![]() Οϊ―ß…ζΘ§Τδ÷–”–
Οϊ―ß…ζΘ§Τδ÷–”–![]() Οϊ―ß…ζΓΑ‘ΡΕΝ ±ΦδΓ±‘Ύ
Οϊ―ß…ζΓΑ‘ΡΕΝ ±ΦδΓ±‘Ύ![]() –Γ ±ΡΎΒΡΗ≈¬ ΈΣ
–Γ ±ΡΎΒΡΗ≈¬ ΈΣ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() .Β±
.Β±![]() »ΓΉν¥σ ±Θ§«σ
»ΓΉν¥σ ±Θ§«σ![]() ΒΡ÷Β.
ΒΡ÷Β.
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©![]() ; Θ®ΔρΘ©
; Θ®ΔρΘ©![]() ;Θ®ΔσΘ©
;Θ®ΔσΘ©![]() .
.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ
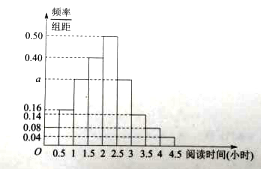
Θ®ΔώΘ©άϊ”ΟΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–Υυ”––ΓΨΊ–ΈΟφΜΐΘ®ΤΒ¬ Θ©÷°ΚΆΈΣ1Ω…«σΒΟ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©÷–ΈΜ ΐΨΆ «Α―÷±ΖΫΆΦΥυ”––ΓΨΊ–ΈΟφΜΐΤΫΖ÷ΒΡΡ«“ΜΒψΘΜ
Θ®ΔσΘ©‘Ύ»Γ≥ωΒΡ![]() Οϊ―ß…ζ÷–Θ§÷ήΡ©‘ΡΕΝ ±Φδ‘Ύ
Οϊ―ß…ζ÷–Θ§÷ήΡ©‘ΡΕΝ ±Φδ‘Ύ![]() ÷–ΒΡ”–
÷–ΒΡ”–![]() »ΥΘ§‘ρ
»ΥΘ§‘ρ![]() Ζΰ¥”ΕΰœνΖ÷≤Φ
Ζΰ¥”ΕΰœνΖ÷≤Φ![]() Θ§”…¥ΥΩ…ΒΟ
Θ§”…¥ΥΩ…ΒΟ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() .”Οœύ≥ΐΖ®
.”Οœύ≥ΐΖ®![]() Ω…«σΒΟ
Ω…«σΒΟ![]() ΒΡΉν¥σ÷ΒΘ°
ΒΡΉν¥σ÷ΒΘ°
‘ΧβΫβΈωΘΚ
Θ®ΔώΘ©
”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§Ω…÷ΣΘ§
÷ήΡ©ΒΡΓΑ‘ΡΕΝ ±ΦδΓ±‘Ύ![]() ΒΡΤΒ¬ ΈΣ
ΒΡΤΒ¬ ΈΣ![]() .
.
Ά§άμΘ§‘Ύ![]() Β»ΉιΒΡΤΒ¬ Ζ÷±πΈΣ
Β»ΉιΒΡΤΒ¬ Ζ÷±πΈΣ![]() Θ§
Θ§
”… ![]()
ΫβΒΟ![]() .
.
Θ®ΔρΘ©…η÷–ΈΜ ΐΈΣ![]() –Γ ±.
–Γ ±.
“ρΈΣ«Α![]() ΉιΒΡΤΒ¬ ÷°ΚΆΈΣ
ΉιΒΡΤΒ¬ ÷°ΚΆΈΣ ![]() Θ§
Θ§
Εχ«Α![]() ΉιΒΡΤΒ¬ ÷°ΚΆΈΣ
ΉιΒΡΤΒ¬ ÷°ΚΆΈΣ ![]() Θ§
Θ§
Υυ“‘![]() .
.
”… ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() .
.
Ι Ω…ΙάΦΤΗΟ–ΘΗΏ“Μ―ß…ζ÷ήΡ©ΓΑ‘ΡΕΝ ±ΦδΓ±ΒΡ÷–ΈΜ ΐΈΣ![]() –Γ ±.
–Γ ±.
Θ®ΔσΘ©…η‘Ύ»Γ≥ωΒΡ![]() Οϊ―ß…ζ÷–Θ§÷ήΡ©‘ΡΕΝ ±Φδ‘Ύ
Οϊ―ß…ζ÷–Θ§÷ήΡ©‘ΡΕΝ ±Φδ‘Ύ![]() ÷–ΒΡ”–
÷–ΒΡ”–![]() »ΥΘ§‘ρ
»ΥΘ§‘ρ![]() Ζΰ¥”ΕΰœνΖ÷≤ΦΘ§Φ¥
Ζΰ¥”ΕΰœνΖ÷≤ΦΘ§Φ¥![]() Θ§‘ρ«ΓΚΟ”–
Θ§‘ρ«ΓΚΟ”–![]() Οϊ―ß…ζ÷ήΡ©‘ΡΕΝ ±Φδ‘Ύ
Οϊ―ß…ζ÷ήΡ©‘ΡΕΝ ±Φδ‘Ύ![]() ÷–ΒΡΗ≈¬ ΈΣ
÷–ΒΡΗ≈¬ ΈΣ
![]() Θ§Τδ÷–
Θ§Τδ÷–![]() .
.
…η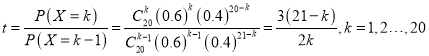 .
.
»τ![]() Θ§‘ρ
Θ§‘ρ![]() ΘΜ
ΘΜ
»τ![]() Θ§‘ρ
Θ§‘ρ![]() .
.
Υυ“‘Β±![]() ±Θ§
±Θ§ ![]() Ήν¥σ.
Ήν¥σ.
Υυ“‘![]() ΒΡ»Γ÷ΒΈΣ
ΒΡ»Γ÷ΒΈΣ![]() .
.


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() .
.
Θ®1Θ©÷ΛΟς![]() ‘Ύ
‘Ύ![]() …œΈΣ‘ωΚ· ΐΘΜ
…œΈΣ‘ωΚ· ΐΘΜ
Θ®2Θ©Β±![]() ±Θ§Ϋβ≤ΜΒ» Ϋ
±Θ§Ϋβ≤ΜΒ» Ϋ![]() ΘΜ
ΘΜ
Θ®3Θ©»τ![]() ‘Ύ
‘Ύ![]() …œΚψ≥…ΝΔΘ§«σ
…œΚψ≥…ΝΔΘ§«σ![]() ΒΡΉν¥σ’ϊ ΐ÷Β.
ΒΡΉν¥σ’ϊ ΐ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΚ· ΐfΘ®xΘ©=x2©¹2x+2‘Ύ«χΦδΘ®0Θ§4]ΒΡ÷Β”ρΈΣΘ® Θ©
A.Θ®2Θ§10]
B.[1Θ§10]
C.Θ®1Θ§10]
D.[2Θ§10]
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΑκΨΕΈΣ5ΒΡ‘≤ΒΡ‘≤–Ρ‘Ύx÷α…œΘ§‘≤–ΡΒΡΚαΉχ±ξ «’ϊ ΐΘ§«“”κ÷±œΏ4x+3y©¹29=0œύ«–Θ°
Θ®ΔώΘ©«σ‘≤ΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©…η÷±œΏax©¹y+5=0Θ®aΘΨ0Θ©”κ‘≤œύΫΜ”ΎAΘ§BΝΫΒψΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®ΔσΘ©‘ΎΘ®ΔρΘ©ΒΡΧθΦΰœ¬Θ§ «Ζώ¥φ‘Ύ Β ΐaΘ§ ΙΒΟœ“ABΒΡ¥Ι÷±ΤΫΖ÷œΏlΙΐΒψPΘ®©¹2Θ§4Θ©Θ§»τ¥φ‘ΎΘ§«σ≥ω Β ΐaΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΚ· ΐfΘ®xΘ©= ![]() ΒΡΕ®“ε”ρΈΣΘ® Θ©
ΒΡΕ®“ε”ρΈΣΘ® Θ©
A.[0Θ§1Θ©
B.[0Θ§2Θ©
C.Θ®1Θ§2Θ©
D.[0Θ§1Θ©Γ»Θ®1Θ§2Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΡ≥ΦΗΚΈΧεΒΡΗ© ”ΆΦ «»γΆΦΥυ ΨΒΡΨΊ–ΈΘ§’ΐ ”ΆΦΘ®Μρ≥Τ÷ς ”ΆΦΘ© «“ΜΗωΒΉ±Ώ≥ΛΈΣ8Θ§ΗΏΈΣ4ΒΡΒ»―ϋ»ΐΫ«–ΈΘ§≤ύ ”ΆΦΘ®Μρ≥ΤΉσ ”ΆΦΘ© «“ΜΗωΒΉ±Ώ≥ΛΈΣ6Θ§ΗΏΈΣ4ΒΡΒ»―ϋ»ΐΫ«–ΈΘ°
Θ®ΔώΘ©«σΗΟΦΗΚΈΧεΒΡΧεΜΐVΘΜ
Θ®ΔρΘ©«σΗΟΦΗΚΈΧεΒΡΟφΜΐSΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤CΘΚ ![]() ΒΡΕΧ÷α≥ΛΈΣ2Θ§άκ–Ρ¬ ΈΣ
ΒΡΕΧ÷α≥ΛΈΣ2Θ§άκ–Ρ¬ ΈΣ ![]() Θ§…ηΙΐ”“ΫΙΒψΒΡ÷±œΏl”κΆ÷‘≤CΫΜ”Ύ≤ΜΆ§ΒΡΝΫΒψAΘ§BΘ§ΙΐAΘ§BΉς÷±œΏx=2ΒΡ¥ΙœΏAPΘ§BQΘ§¥ΙΉψΖ÷±πΈΣPΘ§QΘ°Φ«
Θ§…ηΙΐ”“ΫΙΒψΒΡ÷±œΏl”κΆ÷‘≤CΫΜ”Ύ≤ΜΆ§ΒΡΝΫΒψAΘ§BΘ§ΙΐAΘ§BΉς÷±œΏx=2ΒΡ¥ΙœΏAPΘ§BQΘ§¥ΙΉψΖ÷±πΈΣPΘ§QΘ°Φ« ![]() Θ§»τ÷±œΏlΒΡ–±¬ kΓί
Θ§»τ÷±œΏlΒΡ–±¬ kΓί ![]() Θ§‘ρΠΥΒΡ»Γ÷ΒΖΕΈßΈΣ Θ°
Θ§‘ρΠΥΒΡ»Γ÷ΒΖΕΈßΈΣ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ≤Μ”ΟΦΤΥψΤς«σœ¬Ν–Ης ΫΒΡ÷Β
Θ®1Θ©lg52+ ![]() lg8+lg5lg20+Θ®lg2Θ©2ΘΜ
lg8+lg5lg20+Θ®lg2Θ©2ΘΜ
Θ®2Θ©…η2a=5b=mΘ§«“ ![]() +
+ ![]() =2Θ§«σmΘ°
=2Θ§«σmΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–ΈABCDΚΆΧί–ΈBEFCΥυ‘ΎΤΫΟφΜΞœύ¥Ι÷±Θ§ΓœBCF=ΓœCEF=90ΓψΘ§AD= ![]() Θ°
Θ°
Θ®ΔώΘ©«σ÷ΛΘΚAEΓΈΤΫΟφDCFΘΜ
Θ®ΔρΘ©Β±ABΒΡ≥ΛΈΣΚΈ÷Β ±Θ§ΕΰΟφΫ«A©¹EF©¹CΒΡ¥σ–ΓΈΣ60ΓψΘΩ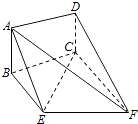
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com