已知二次函数f(x)=2x2-4(a-1)x-a2+2a+9,
(1)若在区间[-1,1]内至少存在一个实数m,使得f(m)>0,求实数a的取值范围;
(2)若对区间[-1,1]内的一切实数m都有f(m)>0,求实数a的取值范围.
分析:(1)根据函数f(x)的对称轴分别表示出f(1),f(-1)和f(a-1),进而根据在区间[-1,1]内至少存在一个实数m,使得f(m)>0,推断函数f(x)的最大值大于0,进而根据a<1时和a≥1时的函数的最大值,求得a的范围;
(2)依题意可知[f(x)]min>0,进而看0≤a≤2和a>2时根据二次函数的单调性求得f(x)的最小值,进而求得a的范围.
解答: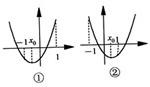
解:∵f(x)的对称轴x
0=a-1,而f(1)=-a
2-2a+15,
f(-1)=-a
2+6a+7,f(a-1)=-3a
2+6a+7;
(1)命题?[f(x)]
max>0,(x∈[-1,1]),
①当x
0<0,即a<1时,[f(x)]
max
=f(1)>0?a
2+2a-15<0?-5<a<3,得-5<a<1;
②当x
0≥0,即a≥1时,[f(x)]
max
=f(-1)>0?a
2-6a-7<0?-1<a<7,得1≤a<7;
综上,a的取值范围是(-5,7);
(2)命题?[f(x)]
min>0(x∈[-1,1]),
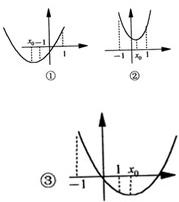
①当x
0<-1,即a<0时,[f(x)]
min
=f(-1)>0?-1<a<7,得-1<a<0;
②当-1≤x
0≤1,即0≤a≤2时,[f(x)]
min
=f(a-1)>0
?3a2-6a-7<0?<a<,
得0≤a≤2;
③当x
0>1,即a>2时,[f(x)]
min=f(1)>0?-5<a<3,
得2<a<3;
综上,a的取值范围是(-1,3).
点评:本题主要考查了函数与方程得综合运用.考查了利用函数的单调性解决方程问题.

 解:∵f(x)的对称轴x0=a-1,而f(1)=-a2-2a+15,
解:∵f(x)的对称轴x0=a-1,而f(1)=-a2-2a+15,


 名校课堂系列答案
名校课堂系列答案