
【题目】已知球的直径![]() ,
,![]() 是该球球面上的两点,
是该球球面上的两点,![]() ,
,![]() ,则棱锥
,则棱锥![]() 的体积为_______.
的体积为_______.
【答案】![]()
【解析】
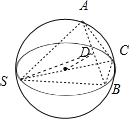
设球心为点O,作AB中点D,连接OD,CD,说明SC是球的直径,利用余弦定理,三角形的面积公式求出S△SCD,和棱锥的高AB,即可求出棱锥的体积.
:设球心为点O,作AB中点D,连接OD,CD.因为线段SC是球的直径,
所以它也是大圆的直径,则易得:∠SAC=∠SBC=90°
所以在Rt△SAC中,SC=4,∠ASC=30° 得:AC=2,SA=2![]()
又在Rt△SBC中,SC=4,∠BSC=30° 得:BC=2,SB=2![]() 则:SA=SB,AC=BC
则:SA=SB,AC=BC
因为点D是AB的中点所以在等腰三角形ASB中,SD⊥AB且SD=![]() =
=![]() =
=![]()
在等腰三角形CAB中,CD⊥AB且CD=![]() =
=![]() =
=![]()
又SD交CD于点D 所以:AB⊥平面SCD 即:棱锥S﹣ABC的体积:V=![]() ABS△SCD,
ABS△SCD,
因为:SD=![]() ,CD=
,CD=![]() ,SC=4 所以由余弦定理得:cos∠SDC=(SD2+CD2﹣SC2)
,SC=4 所以由余弦定理得:cos∠SDC=(SD2+CD2﹣SC2)![]() =(
=(![]() +
+![]() ﹣16)
﹣16)![]() =
=![]() =
=![]()
则:sin∠SDC=![]() =
=![]()
由三角形面积公式得△SCD的面积S=![]() SDCDsin∠SDC=
SDCDsin∠SDC=![]() =3
=3
所以:棱锥S﹣ABC的体积:V=![]() ABS△SCD=
ABS△SCD=![]() =
=![]()
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对心肺疾病入院的![]() 人进行问卷调查,得到了如下的列联表:
人进行问卷调查,得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
(1)用分层抽样的方法在患心肺疾病的人群中抽![]() 人,其中男性抽多少人?
人,其中男性抽多少人?
(2)在上述抽取的![]() 人中选
人中选![]() 人,求恰好有
人,求恰好有![]() 名女性的概率;
名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,你有多大把握认为心肺疾病与性别有关?
,你有多大把握认为心肺疾病与性别有关?
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:  ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
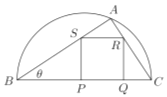
【题目】校园准备绿化一块直径为![]() 的半圆形空地,点
的半圆形空地,点![]() 在半圆圆弧上,△
在半圆圆弧上,△![]() 外的地方种草,△
外的地方种草,△![]() 的内接正方形
的内接正方形![]() 为一水池(
为一水池(![]() ,
,![]() 在
在![]() 边上),其余地方种花,若
边上),其余地方种花,若![]() ,
, ![]() ,设△
,设△![]() 的面积为
的面积为![]() ,正方形面积为
,正方形面积为![]() ;
;
(1)用![]() 和
和![]() 表示
表示![]() 和
和![]() ;
;
(2)当![]() 固定,
固定,![]() 变化时,求
变化时,求![]() 最小值及此时的角
最小值及此时的角![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场按月订购一种家用电暖气,每销售一台获利润200元,未销售的产品返回厂家,每台亏损50元,根据往年的经验,每天的需求量与当天的最低气温有关,如果最低气温位于区间![]() ,需求量为100台;最低气温位于区间
,需求量为100台;最低气温位于区间![]() ,需求量为200台;最低气温位于区间
,需求量为200台;最低气温位于区间![]() ,需求量为300台。公司销售部为了确定11月份的订购计划,统计了前三年11月份各天的最低气温数据,得到下面的频数分布表:
,需求量为300台。公司销售部为了确定11月份的订购计划,统计了前三年11月份各天的最低气温数据,得到下面的频数分布表:
最低气温(℃) |
|
|
|
|
|
天数 | 11 | 25 | 36 | 16 | 2 |
以最低气温位于各区间的频率代替最低气温位于该区间的概率.
求11月份这种电暖气每日需求量![]() (单位:台)的分布列;
(单位:台)的分布列;
若公司销售部以每日销售利润![]() (单位:元)的数学期望为决策依据,计划11月份每日订购200台或250台,两者之中选其一,应选哪个?
(单位:元)的数学期望为决策依据,计划11月份每日订购200台或250台,两者之中选其一,应选哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游风景区发行的纪念章即将投放市场,根据市场调研情况,预计每枚该纪念章的市场价y(单位:元)与上市时间x(单位:天)的数据如下:
上市时间x天 | 2 | 6 | 20 |
市场价y元 | 102 | 78 | 120 |
(1)根据上表数据,从下列函数中选取一个恰当的函数描述该纪念章的市场价y与上市时间x的变化关系并说明理由:①![]() ;②
;②![]() ;③
;③![]() ;
;
(2)利用你选取的函数,求该纪念章市场价最低时的上市天数及最低的价格;
(3)利用你选取的函数,若存在![]() ,使得不等式
,使得不等式![]() 成立,求实数k的取值范围.
成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的最小值及
的最小值及![]() 取到最小值时自变量x的集合;
取到最小值时自变量x的集合;
(2)指出函数y=![]() 的图象可以由函数y=sinx的图象经过哪些变换得到;
的图象可以由函数y=sinx的图象经过哪些变换得到;
(3)当x∈[0,m]时,函数y=f(x)的值域为![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com