练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在Rt△ABC中，已知BC=a若长为2a的线段PQ以点A为中点，问与的夹角Q取何值时·的值最大？并求出这个最大值．

    ??

    解法一：∵⊥，∴·=0，=-，?=-，=∴·=（-）·（-）?=·-·-?·+·?=-a2-·+?·?=-a2+·（-）=-a2+·=-a2+a2cosθ,故当cosθ=1,即θ=0?(与方向相同）时，·最大，其最大值为0.

    解法二：以直角顶点A为坐标原点，两直角边所在直线为坐标轴建立如右图所示的平面直角坐标系.?设|AB|=c,|AC|=b,则A（0，0），B（0，b),（0，b）且|PQ|=2a,?|BC|?=a. 设点P的坐标为（x,y)，则Q（-x,-y).?∴?=(x-c,y), =(-x,-y-b),?=(-c,b)，||=（-2x，-2y）.?∴ ·=（x-c）（-x）+y（-y-b）=-（x2+y2）+cx-by.?∵cosθ=·|?|·||=cx-bya2，∴cx-by=a2cosθ.?∴?·=-a2+a2cosθ.?故当cosθ=1，即θ=0（与方向相同）时，·最大.其最大值为0.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

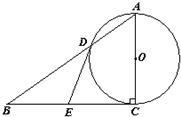    精英家教网如图，在Rt△ABC中，∠C=90°，D为BC上一点，∠DAC=30°，BD=2，AB=2
    		3
    ，则AC的长为（　　）
    A、2
    		2
    B、3
    C、
    		3
    D、
    3
    2
    		3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E．
    （1）求证：点E是边BC的中点；
    （2）若EC=3，BD=2
    		6
    ，求⊙O的直径AC的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

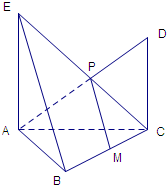    如图，在Rt△ABC中，∠ABC=90°，BA=BC=2，AE⊥平面ABC，CD⊥平面ABC，CE交AD于点P．
    （1）若AE=CD，点M为BC的中点，求证：直线MP∥平面EAB
    （2）若AE=2，CD=1，求锐二面角E-BC-A的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    8．如图，在Rt△ABC中，∠CAB=90°，AB=2，AC=
    		2
    2
    ．DO⊥AB于O点，OA=OB，DO=2，曲线E过C点，动点P在E上运动，且保持|PA|+|PB|的值不变．
    （1）建立适当的坐标系，求曲线E的方程；
    （2）过D点的直线L与曲线E相交于不同的两点M、N且M在D、N之间，设
    DM
    DN
    =λ，试确定实数λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

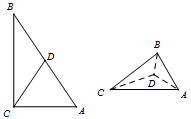    精英家教网如图，在Rt△ABC中，AC=1，BC=x，D是斜边AB的中点，将△BCD沿直线CD翻折，若在翻折过程中存在某个位置，使得CB⊥AD，则x的取值范围是（　　）
    A、（0，
    		3
    ]
    B、（
    		2
    2
    ，2]
    C、（
    		3
    ，2
    		3
    ]
    D、（2，4]

    查看答案和解析>>

    同步练习册答案