
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 的极值点;
的极值点;
(2)求方程![]() 的根的个数.
的根的个数.
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
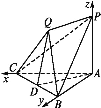
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,△ABC是直角三角形,且PA=AB=AC.又平面QBC垂直于底面ABC.
(1)求证:PA∥平面QBC;
(2)若PQ⊥平面QBC,求锐二面角Q-PB-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某啤酒厂要将一批鲜啤酒用汽车从所在城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,运费由厂家承担.若厂家恰能在约定日期(×月×日)将啤酒送到,则城市乙的销售商一次性支付给厂家40万元;若在约定日期前送到,每提前一天销售商将多支付给厂家2万;若在约定日期后送到,每迟到一天销售商将少支付给厂家2万元.为保证啤酒新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送.已知下表内的信息:
汽车行驶路线 | 在不堵车的情况下到达城市乙所需时间(天) | 在堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
公路1 | 1 | 4 |
| 2 |
公路2 | 2 | 3 |
| 1 |
(1)记汽车选择公路1运送啤酒时厂家获得的毛收入为X(单位:万元),求X的分布列和EX;
(2)若![]() ,
,![]() ,选择哪条公路运送啤酒厂家获得的毛收人更多?
,选择哪条公路运送啤酒厂家获得的毛收人更多?
(注:毛收入=销售商支付给厂家的费用-运费).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)六个从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有几种?
(2)把5件不同产品摆成一排,若产品![]() 与产品
与产品![]() 相邻,且产品
相邻,且产品![]() 与产品
与产品![]() 不相邻,则不同的摆法有几种?
不相邻,则不同的摆法有几种?
(3)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法有几种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆C:
中,已知椭圆C:![]() (
(![]() >
>![]() >0)的右焦点为F(1,0),且过点(1,
>0)的右焦点为F(1,0),且过点(1,![]() ),过点F且不与
),过点F且不与![]() 轴重合的直线
轴重合的直线![]() 与椭圆C交于A,B两点,点P在椭圆上,且满足
与椭圆C交于A,B两点,点P在椭圆上,且满足![]() .
.
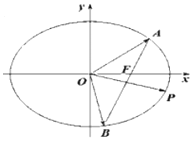
(1)求椭圆C的标准方程;
(2)若![]() ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图像上有动点
图像上有动点![]() ,函数
,函数![]() 图像上有动点
图像上有动点![]() .若
.若![]() 两点同时从纵坐标
两点同时从纵坐标![]() 的初始位置出发,沿着各自函数图像向右上方运动至
的初始位置出发,沿着各自函数图像向右上方运动至![]() 两点的纵坐标值再次相等,且始终满足
两点的纵坐标值再次相等,且始终满足![]() ,则在此运动过程中
,则在此运动过程中![]() 两点的距离
两点的距离![]() 的取值范围是______.
的取值范围是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com