
【题目】如图,在正四棱锥![]() 中,O为顶点S在底面ABCD内的投影,P为侧棱SD的中点,且
中,O为顶点S在底面ABCD内的投影,P为侧棱SD的中点,且![]() .
.
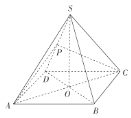
(1)证明:![]() 平面PAC.
平面PAC.
(2)求直线BC与平面PAC的所成角的大小.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OP,可得![]() ,利用线面平行的判定定理即可证出.
,利用线面平行的判定定理即可证出.
(2)以O为坐标原点,以OA所在直线为x轴,OB所在直线为y轴,OS所在直线为z轴,建立空间直角坐标系![]() ,设
,设![]() ,求出平面PAC的一个法向量,利用向量的数量积结合图形即可求解.
,求出平面PAC的一个法向量,利用向量的数量积结合图形即可求解.
(1)证明:连接OP,因为O,P分别为BD和SD的中点,所以![]() ,
,
又![]() 平面PAC,
平面PAC,![]() 平面PAC,所以
平面PAC,所以![]() 平面PAC.
平面PAC.
(2)解:如图,以O为坐标原点,以OA所在直线为x轴,OB所在直线为y轴,
OS所在直线为z轴,建立空间直角坐标系![]() .
.
设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
设平面PAC的一个法向量为![]() ,
,
则![]() ,
,![]() ,
,
所以![]() ,令
,令![]() ,得
,得![]() ,
,
所以
所以![]()
故直线BC与平面PAC的夹角为![]() .
.


科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,以原点![]() 为圆心,
为圆心,![]()
![]() 为半径的定圆
为半径的定圆![]() ,与过原点且斜率为
,与过原点且斜率为![]()
![]() 的动直线交于
的动直线交于![]() 、
、![]() 两点,在
两点,在![]() 轴正半轴上有一个定点
轴正半轴上有一个定点![]() ,
,![]() 、
、![]() 、
、![]() 三点构成三角形,求:
三点构成三角形,求:
(1)△![]() 的面积
的面积![]() 的表达式,并求出
的表达式,并求出![]() 的取值范围;
的取值范围;
(2)△![]() 的外接圆
的外接圆![]() 的面积
的面积![]() 的表达式,并求出
的表达式,并求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,过其焦点
,过其焦点![]() 作斜率为1的直线交抛物线
作斜率为1的直线交抛物线![]() 于
于![]() ,
,![]() 两点,且线段
两点,且线段![]() 的中点的纵坐标为4.
的中点的纵坐标为4.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若不过原点![]() 且斜率存在的直线
且斜率存在的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() .求证:直线
.求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 经过点
经过点![]() .设椭圆
.设椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,右准线与
,右准线与![]() 轴交于点
轴交于点![]() ,且
,且![]() 为线段
为线段![]() 的中点.
的中点.
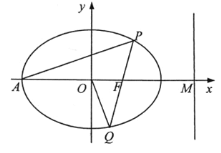
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() (
(![]() 在
在![]() 轴上方),直线
轴上方),直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,且直线
,且直线![]() 与
与![]() 垂直,求直线
垂直,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为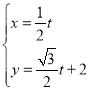 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求直线![]() 被曲线
被曲线![]() 所截得的弦长.
所截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校针对校食堂饭菜质量开展问卷调查,提供满意与不满意两种回答,调查结果如下表(单位:人):
学生 | 高一 | 高二 | 高三 |
满意 | 500 | 600 | 900 |
不满意 | 300 | 200 | 300 |
(1)求从所有参与调查的人中任选1人是高三学生的概率;
(2)从参与调查的高三学生中,用分层抽样的方法抽取4人,在这4人中任意选取2人,求这两人对校食堂饭菜质量都满意的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.某班![]() 位同学从文学、经济和科技三类不同的图书中任选一类,不同的结果共有
位同学从文学、经济和科技三类不同的图书中任选一类,不同的结果共有![]() 种;
种;
B.甲乙两人独立地解题,已知各人能解出的概率分别是![]() ,则题被解出的概率是
,则题被解出的概率是![]() ;
;
C.某校![]() 名教师的职称分布情况如下:高级占比
名教师的职称分布情况如下:高级占比![]() ,中级占比
,中级占比![]() ,初级占比
,初级占比![]() ,现从中抽取
,现从中抽取![]() 名教师做样本,若采用分层抽样方法,则高级教师应抽取
名教师做样本,若采用分层抽样方法,则高级教师应抽取![]() 人;
人;
D.两位男生和两位女生随机排成一列,则两位女生不相邻的概率是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据新高考改革方案,某地高考由文理分科考试变为“3+3”模式考试.某学校为了解高一年425名学生选课情况,在高一年下学期进行模拟选课,统计得到选课组合排名前4种如下表所示,其中物理、化学、生物为理科,政治、历史、地理为文科,“√”表示选择该科,“×”表示未选择该科,根据统计数据,下列判断错误的是
学科 人数 | 物理 | 化学 | 生物 | 政治 | 历史 | 地理 |
124 | √ | √ | × | × | × | √ |
101 | × | × | √ | × | √ | √ |
86 | × | √ | √ | × | × | √ |
74 | √ | × | √ | × | √ | × |
A. 前4种组合中,选择生物学科的学生更倾向选择两理一文组合
B. 前4种组合中,选择两理一文的人数多于选择两文一理的人数
C. 整个高一年段,选择地理学科的人数多于选择其他任一学科的人数
D. 整个高一年段,选择物理学科的人数多于选择生物学科的人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com