
分析 通过设z=a+bi、$\overline{z}$=a-bi,代入|z|-$\overline{z}$=2+4i,利用复数相等计算即可.
解答 解:设z=a+bi,则$\overline{z}$=a-bi,
∵|z|-$\overline{z}$=2+4i,
∴$\sqrt{{a}^{2}+{b}^{2}}$-(a-bi)=($\sqrt{{a}^{2}+{b}^{2}}$-a)+bi=2+4i,
∴$\left\{\begin{array}{l}{\sqrt{{a}^{2}+{b}^{2}}-a=2}\\{b=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=3}\\{b=4}\end{array}\right.$,
∴z=3+4i,
故答案为:3+4i.
点评 本题考查复数求模,利用复数相等是解决本题的关键,注意解题方法的积累,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
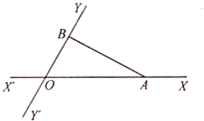 如图,有两条相交成60°角的直路XX′,YY′,交点是O,甲和乙同时从点O出发,甲沿着OX的方向,乙沿着OY的方向,经过若干小时后,甲到达点A,乙到达点B,此时甲测得他走过的路程比他到乙的距离多2km,且乙走过的路程超过4km,设甲到达点A,乙到达点B时,乙走过的路程为x km,甲走过的路程为y km.
如图,有两条相交成60°角的直路XX′,YY′,交点是O,甲和乙同时从点O出发,甲沿着OX的方向,乙沿着OY的方向,经过若干小时后,甲到达点A,乙到达点B,此时甲测得他走过的路程比他到乙的距离多2km,且乙走过的路程超过4km,设甲到达点A,乙到达点B时,乙走过的路程为x km,甲走过的路程为y km.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 等级 | 1 | 2 | 3 | 4 |
| 频率 | m | n | 0.5 | 0.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com