Question

14．在平行六面体ABCD-A₁B₁C₁D₁中，AB=1，AD=1，AA₁=2，∠BAD=90°，∠BAA₁=∠DAA₁=60°，则AC₁的长为（　　）

• A． $\sqrt{13}$
• B． $\sqrt{5}$
• C． $\sqrt{10}$
• D． 2+$\sqrt{3}$

Answer 1

分析 利用空间向量，表示$\overrightarrow{A{C}_{1}}$，再由AB=1，AD=1，AA₁=2，∠BAD=，90°，∠BAA₁=∠DAA₁=60°，通过向量的模能求出结果．

解答 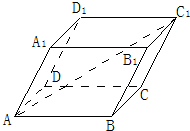解：在平行六面体ABCD-A₁B₁C₁D₁中，
∵AB=1，AD=1，AA₁=2，∠BAD=90°，∠BAA₁=∠DAA₁=60°，$\overrightarrow{A{C}_{1}}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{C{C}_{1}}$，
∴$\overrightarrow{A{C}_{1}}$²=${\overrightarrow{AB}}^{2}$+${\overrightarrow{BC}}^{2}$+${\overrightarrow{C{C}_{1}}}^{2}$+2$\overrightarrow{AB}•\overrightarrow{BC}$+2$\overrightarrow{AB}•\overrightarrow{C{C}_{1}}$+2$\overrightarrow{BC}•\overrightarrow{C{C}_{1}}$
=1+1+4+0+2×1×2×cos60°+2×1×2×cos60°
=10，
∴|$\overrightarrow{A{C}_{1}}$|=$\sqrt{10}$．
故选：C．

点评 本题考查棱柱的结构特征，是基础题．解题时要认真审题，仔细解答，注意向量法的合理运用．如本题这样，基向量的夹角与模已知，用向量法求线段长度是最优选择．