
(Ⅰ)写出双曲线C的离心率![]() 与
与![]() 的关系式;
的关系式;
(Ⅱ)当![]() 时,经过焦点F且平行于OP的直线交双曲线于A、B点,若
时,经过焦点F且平行于OP的直线交双曲线于A、B点,若![]() ,求此时的双曲线方程。
,求此时的双曲线方程。

(22)本小题主要考查直线方程、双曲线的几何性质等基本知识,考查综合运用数学知识解决问题的能力及推理能力.

(Ⅰ)解法1:设![]() 为
为![]() 与双曲线右准线的交点,
与双曲线右准线的交点,![]() 则
则
![]()
![]()
![]()
![]()
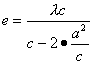 .
.
即![]()
解法2:设![]() 为PM与双曲线右准线的交点,N为左准线与x轴的交点,F(c,0),P(
为PM与双曲线右准线的交点,N为左准线与x轴的交点,F(c,0),P(![]() ),由于P(
),由于P(![]() )在双曲线右支上,则
)在双曲线右支上,则
![]() ①
①
![]() ②
②
由|PF|=![]() 得
得
![]() ③
③
由①、②代入③得
![]()
再将c=ea,b=a![]() 代入上式,得
代入上式,得
![]()
化简,得
![]() ④
④
由题意,点P位于双曲线右支上,从而
|PM|>|M![]() |.
|.
于是![]() 解得e=2,
解得e=2,
从而c=2a,b=![]()
由此得双曲线的方程是
![]() .
.
下面确定a的值。
解法1:
设双曲线左准线与x轴的交点为N,P点的坐标为(![]() ),则
),则
|ON|=![]()
|MN|=![]()
由于P(![]() )在双曲线的右支上,且位于x轴上方,因而
)在双曲线的右支上,且位于x轴上方,因而
![]()
所以直线OP的斜率为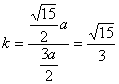 。
。
设过焦点F且平行于OP的直线与双曲线的交点为A(![]() )、B(
)、B(![]() ),则直线AB的斜率为
),则直线AB的斜率为![]() ,直线AB的方程为
,直线AB的方程为
![]()
将其代入双曲线方程整理得
![]()
∵ ![]()
∴ |AB|=![]()
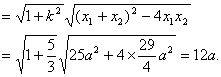
由|AB|=12得a=1.于是,所求双曲线的方程为
![]()
解法2:由条件![]() OFPM为菱形,其对角线OP与FM互相垂直平分,其交点Q为OP的中点。
OFPM为菱形,其对角线OP与FM互相垂直平分,其交点Q为OP的中点。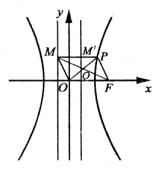
设OP的方程为![]() 则FM的方程为
则FM的方程为
![]()
由 解得Q点的坐标为(
解得Q点的坐标为(![]() ),
),
所以P点的坐标为(![]() ).
).
将P点的坐标代入双曲线方程,化简得
![]()
解得![]()
设过焦点F且平行于OP的直线与双曲线的交点为![]() 、
、![]() ,则直线AB的斜率为
,则直线AB的斜率为![]() ,直线AB的方程为
,直线AB的方程为
![]()
将其代入双曲线方程,整理得
![]()
∵ ![]()
∴
![]()
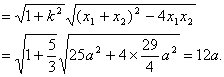
由|AB|=12得a=1.于是,所求双曲线的方程为
![]()


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
 如图,F为双曲线C:
如图,F为双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
| PF |
| OF |
查看答案和解析>>
科目:高中数学 来源: 题型:
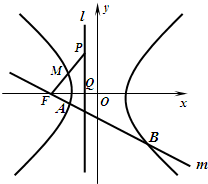 如图点F为双曲线C的左焦点,左准线l交x轴于点Q,点P是l上的一点|PQ|=|FQ|=1,且线段PF的中点M在双曲线C的左支上.
如图点F为双曲线C的左焦点,左准线l交x轴于点Q,点P是l上的一点|PQ|=|FQ|=1,且线段PF的中点M在双曲线C的左支上.| FB |
| FA |
查看答案和解析>>
科目:高中数学 来源: 题型:
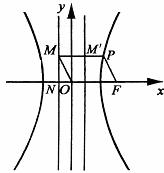
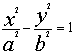 (a>0,b>0)的右焦点,P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为平行四边形,|PF|=
(a>0,b>0)的右焦点,P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为平行四边形,|PF|=(Ⅰ)写出双曲线C的离心率e与![]() 的关系式:
的关系式:
(Ⅱ)写![]() =1时,经过焦点F且平行于OP的直线交双曲线于A、B两点,若|AB|=12,求此时的双曲线方程。
=1时,经过焦点F且平行于OP的直线交双曲线于A、B两点,若|AB|=12,求此时的双曲线方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com