
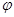 (x)=
(x)=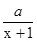 ,a是正常数。(1)若f(x)=
,a是正常数。(1)若f(x)= 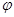 (x)+lnx,且a=
(x)+lnx,且a=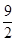 ,求函数f(x)的单调递增区间;(2)若g(x)=∣lnx∣+
,求函数f(x)的单调递增区间;(2)若g(x)=∣lnx∣+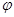 (x),且对任意的x
(x),且对任意的x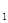 ,x
,x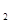 ∈(0,2〕,且x
∈(0,2〕,且x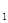 ≠x
≠x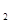 ,都有
,都有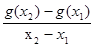 <-1,求a的取值范围
<-1,求a的取值范围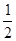 )和(2,+∞)(2)
)和(2,+∞)(2)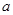 ≧
≧
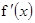 =
=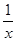 -
-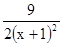 ﹥1
﹥1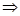
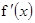 =
=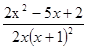 ﹥0
﹥0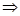 x﹥2或0﹤x﹤
x﹥2或0﹤x﹤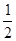 ,
,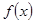 的单调增区间为(0,
的单调增区间为(0,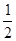 )和(2,+∞)……………………………3分
)和(2,+∞)……………………………3分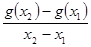 ﹤-1,所以
﹤-1,所以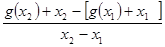 ﹤0,
﹤0,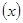 =
=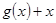 在区间(0,2】上是减函数。
在区间(0,2】上是减函数。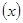 =ln
=ln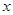 +
+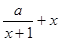
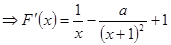 ,
,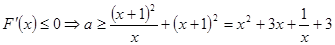 在x∈
在x∈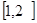 上恒成立。
上恒成立。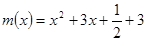 ,所以
,所以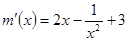 ﹥0(1≦x≦2),
﹥0(1≦x≦2), 在[1,2]上为增函数,所以
在[1,2]上为增函数,所以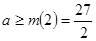
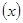 =-ln
=-ln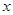 +
+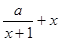
 ,
,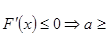 -
-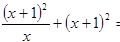 =
=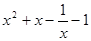 在x∈(0,1)上恒成立。
在x∈(0,1)上恒成立。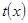 =
=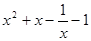
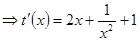 ﹥0,所以
﹥0,所以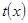 在(0,1)上为增函数,所以
在(0,1)上为增函数,所以 ,综上:
,综上: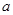 的取值范围为
的取值范围为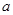 ≧
≧ …………………12分
…………………12分

科目:高中数学 来源:不详 题型:填空题
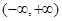 上的偶函数
上的偶函数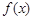 满足:
满足: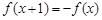 ,且在
,且在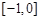 上是增函数,下面关于
上是增函数,下面关于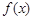 的判断:
的判断: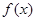 是周期函数;
是周期函数; 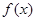 的图象关于直线
的图象关于直线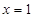 对称;
对称;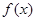 在
在 上是增函数;
上是增函数; 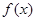 在
在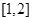 上是减函数;
上是减函数;  .
. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com