
设![]() ,
,![]() ,函数
,函数![]() ,
,
(1)设不等式![]() 的解集为C,当
的解集为C,当![]() 时,求实数
时,求实数![]() 取值范围;
取值范围;
(2)若对任意![]() ,都有
,都有![]() 成立,试求
成立,试求![]() 时,
时,![]() 的值
的值![]() 域;
域;
(3)设![]()
![]() ,求
,求![]() 的最小值.
的最小值.
解:(1)![]() ,因为
,因为![]() ,二次函数
,二次函数![]() 图像开口向上,且
图像开口向上,且![]() 恒成立,故图像始终与
恒成立,故图像始终与![]() 轴有两个交点,由题意,要使这两个交点横坐标
轴有两个交点,由题意,要使这两个交点横坐标![]() ,当且仅当:
,当且仅当:
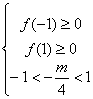 , …………………………4分
, …………………………4分
解得:![]() …………………………5分
…………………………5分
(2)对任意![]() 都有
都有![]() ,所以
,所以![]() 图像关于直线
图像关于直线![]() 对称,
对称,
所以![]() ,得
,得![]() . …………………………7分
. …………………………7分
所以![]() 为
为![]() 上减函数.
上减函数.
![]() ;
;![]() .故
.故![]() 时,
时,![]() 值域为
值域为![]() .
.
…………………………9分
(3)令![]() ,则
,则![]()
(i)当![]() 时,
时,![]() ,
,
当![]() ,则函数
,则函数![]() 在
在![]() 上单调递减,
上单调递减,
从而函数![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
若![]() ,则函数
,则函数![]() 在
在![]() 上
上![]() 的最小值为
的最小值为![]() ,且
,且![]() .
.
…………………………12分
(ii)当![]() 时,函数
时,函数![]()
若![]() ,则函数
,则函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,且
,且![]()
若![]() ,则函数
,则函数![]() 在
在![]() 上单调递增,
上单调递增,
从而函数![]() 在
在![]() 上的最小值为
上的最小值为![]() .…………………………15分
.…………………………15分
综上,当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]()
当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() [来源:学#科#网Z#X#X#K]
[来源:学#科#网Z#X#X#K]
当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() . …………………………16分
. …………………………16分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 已知常数c>0.根据如图的程序框图:
已知常数c>0.根据如图的程序框图:查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013届度江西南昌二中高二下学期期末理科数学试卷(解析版) 题型:解答题
(本题13分)设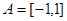 ,
,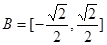 ,函数
,函数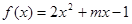 ,
,
(1)设不等式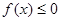 的解集为C,当
的解集为C,当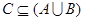 时,求实数
时,求实数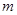 取值范围;
取值范围;
(2)若对任意 ,都有
,都有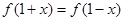 成立,求
成立,求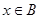 时,
时,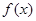 的值域;
的值域;
(3)设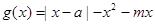
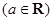 ,求
,求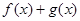 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2013届江苏省扬州市邗江区高二下学期期中考试数学试卷(解析版) 题型:解答题
设 ,
, ,函数
,函数 ,
,
(1)设不等式 的解集为C,当
的解集为C,当 时,求实数
时,求实数 取值范围;
取值范围;
(2)若对任意 ,都有
,都有 成立,试求
成立,试求 时,
时, 的值域;
的值域;
(3)设
 ,求
,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:黑龙江省2012届高二下学期期末考试数学(理) 题型:解答题
(12分)设命题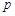 :函数
:函数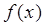 =x3-ax-1在区间
=x3-ax-1在区间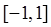 上单调递减;命题
上单调递减;命题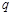 :函数
:函数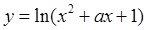 的值域是
的值域是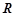 .如果命题
.如果命题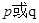 为真命题,
为真命题,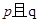 为假命题,求
为假命题,求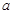 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com