
某单位 名员工参加“社区低碳你我他”活动.他们的年龄在
名员工参加“社区低碳你我他”活动.他们的年龄在 岁至
岁至 岁
岁
之间.按年龄分组:第1组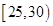 ,第
,第 组
组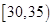 ,第3组
,第3组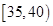 ,第
,第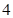 组
组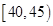 ,第
,第 组
组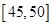 ,得到的频率分布直方图如图所示.下表是年龄的频率分布表.
,得到的频率分布直方图如图所示.下表是年龄的频率分布表.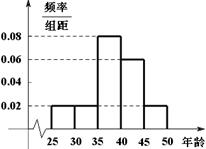
| 区间 | 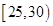 | 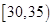 | 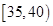 | 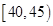 | 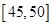 |
| 人数 |  |  |  | | |
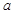 、
、 、
、 的值;
的值; 、
、 、
、 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取 人,则年龄在第
人,则年龄在第 、
、 、
、 组的人数分别
组的人数分别 人中随机抽取
人中随机抽取 人参加社区宣传交流活动,求恰有
人参加社区宣传交流活动,求恰有 人在第
人在第 组的概率.
组的概率. (1)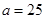 ,
,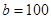 ,
,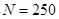 ;(2)
;(2) 、
、 、
、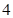 ;(3)
;(3)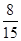 .
.
解析试题分析:(1)先利用频率分布直方图的特点得到第一组和第二组的人数相同,从而得到 的值,然后利用分层抽样中各层的入样比相等求出
的值,然后利用分层抽样中各层的入样比相等求出 的值,最后利用频率、频数以及样本容量三者之间的关系求出
的值,最后利用频率、频数以及样本容量三者之间的关系求出 的值;(2)先确定
的值;(2)先确定 、
、 、
、 组的总人数,然后利用入样比算出每组所抽取的人数;(3)先将各组所抽取的人进行编号,然后列举法找出样本空间以及题中涉及的事件所包含的基本事件及数目,最后利用古典概型的概率计算公式计算事件发生的概率.
组的总人数,然后利用入样比算出每组所抽取的人数;(3)先将各组所抽取的人进行编号,然后列举法找出样本空间以及题中涉及的事件所包含的基本事件及数目,最后利用古典概型的概率计算公式计算事件发生的概率.
试题解析:(1)由频率分布直方图可知,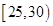 与
与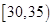 两组的人数相同,所以
两组的人数相同,所以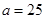 人.
人.
且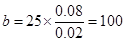 人.总人数
人.总人数 人.
人.
(2)因为第 、
、 、
、 组共有
组共有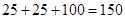 人,利用分层抽样在
人,利用分层抽样在 名员工中抽取
名员工中抽取 人,每组抽取的
人,每组抽取的
人数分别为:
第 组的人数为
组的人数为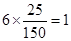 ,第
,第 组的人数为
组的人数为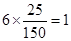 , 第
, 第 组的人数为
组的人数为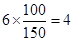 ,
,
所以第 、
、 、
、 组分别抽取
组分别抽取 人,
人, 人,
人,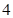 人;
人;
(3)由(2)可设第 组的
组的 人为
人为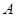 ,第
,第 组的
组的 人为
人为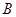 ,第
,第 组的
组的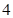 人分别为
人分别为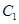 、
、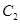 、
、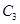 、
、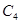 ,则从
,则从
人中抽取 人的所有可能结果为:
人的所有可能结果为: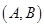 ,
,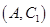 ,
,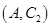 ,
,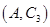 ,
,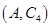 ,
, ,
,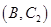 ,
,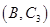 ,
,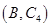 ,
,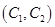 ,
,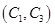 ,
, ,
,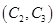 ,
,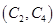 ,
,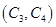 ,共有
,共有 种.
种.
其中恰有 人年龄在第
人年龄在第 组的所有结果为:
组的所有结果为: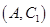 ,
,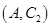 ,
,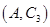 ,
,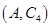 ,
, ,
,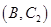 ,
,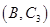 ,
,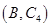 ,共有
,共有 种.
种.
所以恰有 人年龄在第
人年龄在第 组的概率为
组的概率为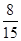 .
.
考点:1.频率分布直方图;2.分层抽样;3.古典概型


科目:高中数学 来源: 题型:解答题
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
(1)求n的值;
(2)把在前排就坐的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖,.求a和b至少有一人上台抽奖的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以 表示.
表示.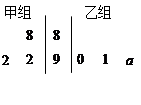
(Ⅰ)若甲、乙两个小组的数学平均成绩相同,求 的值;
的值;
(Ⅱ)求乙组平均成绩超过甲组平均成绩的概率;
(Ⅲ)当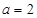 时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作。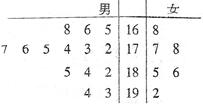
(I)求男生成绩的中位数及女生成绩的平均值;
(II)如果用分层抽样的方法从“甲部门”人选和“乙部门”人选中共选取5人,再从这5人中选2人,那么至少有一人是“甲部门”人选的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2013年12月21日上午10时,省会首次启动重污染天气Ⅱ级应急响应,正式实施机车尾号限行,当天某报社为了解公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(1)完成被调查人员的频率分布直方图;
(2)若从年龄在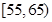 ,
,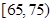 的被调查者中各随机选取1人进行追踪调查,求两人中至少有1人赞成“车辆限行”的概率.
的被调查者中各随机选取1人进行追踪调查,求两人中至少有1人赞成“车辆限行”的概率. 
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念性指数值,交通指数取值范围为0~10,分为五个级别,0~2 畅 通;2~4 基本畅通;4~6 轻度拥堵;6~8 中度拥堵;8~10 严重拥堵 早高峰时段,从昆明市交通指挥中心随机选取了二环以内的50个交通路段,依据其交通指数数据绘制的直方图如图 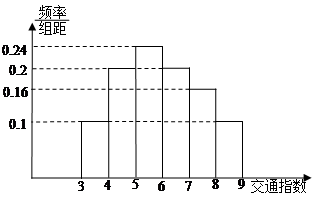
(1)据此估计,早高峰二环以内的三个路段至少有一个是严重拥堵的概率是多少?
(2)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟;中度拥堵为42分钟;严重拥堵为60分钟,求此人所用时间的数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高三文科分为五个班.高三数学测试后, 随机地在各班抽取部分学生进行成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了18人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.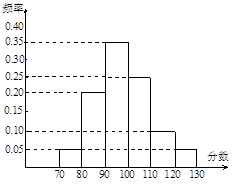
(1)问各班被抽取的学生人数各为多少人?
(2)在抽取的所有学生中,任取一名学生,求分数不小于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如图所示:
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm的概率;
(3)从样本中身高在180~190cm的男生中任选2人,求至少有1人身高在185~190cm的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
南昌市为增强市民的交通安全意识,面向全市征召“小红帽”志愿者在部分交通路口协助交警维持交通,把符合条件的1000名志愿者按年龄分组:第1组 、第2组
、第2组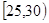 、第3组
、第3组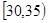 、第4组
、第4组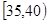 、第5组
、第5组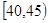 ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
(1)若从第3、4、5组中用分层抽样的方法抽取12名志愿者在五一节这天到广场协助交警维持交通,应从第3、4、5组各抽取多少名志愿者?
(2)在(1)的条件下,南昌市决定在这12名志愿者中在第四或第五组的志愿者中,随机抽取3名志愿者到学校宣讲交通安全知识,求到学校宣讲交通知识的资源者中恰好1名市第五组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com