
【题目】给出下列命题:
①点P(-1,4)到直线3x+4y =2的距离为3.
②过点M(-3,5)且在两坐标轴上的截距互为相反数的直线方程为![]() .
.
③命题“x∈R,使得x2﹣2x+1<0”的否定是真命题;
④“x ≤1,且y≤1”是“x + y ≤2”的充要条件.
其中不正确命题的序号是 _______________ .(把你认为不正确命题的序号都填上)
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图所示,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB的中点,且△PDB是正三角形,PA⊥PC.
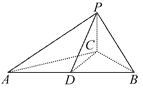
(1)求证:平面PAC⊥平面ABC.
(2)求二面角D-AP-C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某小区准备将闲置的一直角三角形(其中∠B=![]() ,AB=a,BC=
,AB=a,BC=![]() a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.
a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.
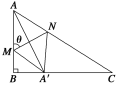
(1)若θ=![]() 时,绿地“最美”,求最美绿地的面积;
时,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民的行走,设计时要求将AN,A′N的值设计最短,求此时绿地公共走道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(其中16名女员工,14名男员工)的得分,如下表:
女 | 47 36 32 48 34 44 43 47 46 41 43 42 50 43 35 49 |
男 | 37 35 34 43 46 36 38 40 39 32 48 33 40 34 |
(Ⅰ)现求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
“满意”的人数 | “不满意”的人数 | 合计 | |
女 | 16 | ||
男 | 14 | ||
合计 | 30 |
(Ⅱ)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关?
参考数据:
| 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考公式:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某班一次数学测试成绩的茎叶图(如图甲)和频率分布直方图(如图乙)都受到不同程度的污损,其中,频率分布直方图的分组区间分别为![]() ,据此解答如下问题.(注:直方图中
,据此解答如下问题.(注:直方图中![]() 与
与![]() 对应的长方形的高度一样)
对应的长方形的高度一样)
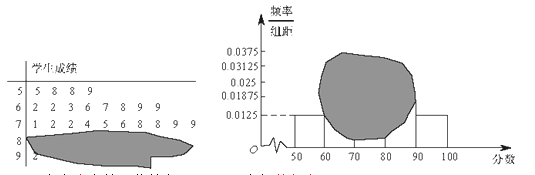
(1)若按题中的分组情况进行分层抽样,共抽取![]() 人,那么成绩在
人,那么成绩在![]() 之间应抽取多少人?
之间应抽取多少人?
(2)现从分数在![]() 之间的试卷中任取
之间的试卷中任取![]() 份分析学生失分情况,设抽取的试卷分数在
份分析学生失分情况,设抽取的试卷分数在![]() 之间 份数为
之间 份数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知(x+![]() )n展开式的二项式系数之和为256
)n展开式的二项式系数之和为256
(1)求n;
(2)若展开式中常数项为![]() ,求m的值;
,求m的值;
(3)若展开式中系数最大项只有第6项和第7项,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com