
【题目】已知中心在原点,焦点在 ![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点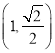 ,离心率为
,离心率为![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 的长轴的两个端点(
的长轴的两个端点(![]() 位于
位于![]() 右侧),
右侧),![]() 是椭圆在
是椭圆在![]() 轴正半轴上的顶点.
轴正半轴上的顶点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 和
和![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出直线方程;如果不存在,请说明理由.
共线?如果存在,求出直线方程;如果不存在,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的标准方程为
的标准方程为![]() ,离心率
,离心率![]() ,且椭圆经过点
,且椭圆经过点![]() .过右焦点
.过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,求直线
,求直线![]() 的方程.
的方程.
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() ,
, ![]() 为邻边的四边形
为邻边的四边形![]() 是菱形,且点
是菱形,且点![]() 在椭圆上.若存在,求出
在椭圆上.若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的快速发展,民用汽车的保有量也迅速增长.机动车保有量的发展影响到环境质量、交通安全、道路建设等诸多方面.在我国,尤其是大中型城市,机动车已成为城市空气污染的重要来源.因此,合理预测机动车保有量是未来进行机动车污染防治规划、道路发展规划等的重要前提.从2012年到2016年,根据“云南省某市国民经济和社会发展统计公报”中公布的数据,该市机动车保有量数据如表所示.
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
机动车保有量 | 169 | 181 | 196 | 215 | 230 |
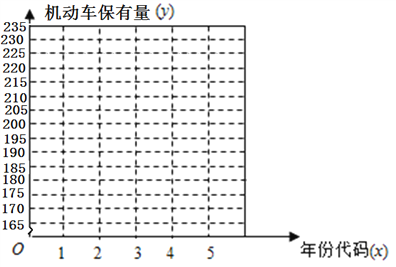
(1)在图所给的坐标系中作出数据对应的散点图;
(2)建立机动车保有量![]() 关于年份代码
关于年份代码![]() 的回归方程;
的回归方程;
(3)按照当前的变化趋势,预测2017年该市机动车保有量.
附注:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
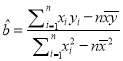 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,满足![]() .
.
(1)求角C的大小;
(2)设函数f(x)=cos(2x+C),将f(x)的图象向右平移![]() 个单位长度后得到函数g(x)的图象,求函数g(x)在区间
个单位长度后得到函数g(x)的图象,求函数g(x)在区间![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() 为整数,且对任意
为整数,且对任意![]() 都有
都有![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,
, 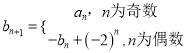 求
求![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在(2)的条件下,若数列![]() 满足
满足![]() .是否存在实数
.是否存在实数![]() ,使得数列
,使得数列![]() 是单调递增数列.若存在,求出
是单调递增数列.若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率
,且离心率![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若椭圆![]() 上存在点
上存在点![]() 、
、![]() 关于直线
关于直线![]() 对称,求
对称,求![]() 的所有取值构成的集合
的所有取值构成的集合![]() ,并证明对于
,并证明对于![]() ,
, ![]() 的中点恒在一条定直线上.
的中点恒在一条定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com