解:(1)因为函数f(x)=ln(e
x+k)(k为常数)是实数集R上的奇函数,
所以f(-0)=-f(0)即f(0)=0,
则ln(e
0+k)=0解得k=0,
显然k=0时,f(x)=x是实数集R上的奇函数;
(2)由(1)得f(x)=x所以g(x)=λx+sinx,g'(x)=λ+cosx,
因为g(x) 在[-1,1]上单调递减,∴g'(x)=λ+cosx≤0 在[-1,1]上恒成立,
∴λ≤-1,g(x)
max=g(-1)=-λ-sin1,
只需-λ-sin1≤t
2+λt+1(λ≤-1),
∴(t+1)λ+t
2+sin1+1≥0(λ≤-1)恒成立,
令h(λ)=(t+1)λ+t
2+sin1+1(λ≤-1)
则
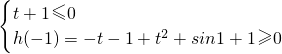
解得t≤-1
(3)由(1)得f(x)=x
∴方程转化为

=x
2-2ex+m,令F(x)=

(x>0),G(x)=x
2-2ex+m (x>0),(8分)
∵F'(x)=

,令F'(x)=0,即

=0,得x=e
当x∈(0,e)时,F'(x)>0,∴F(x)在(0,e)上为增函数;
当x∈(e,+∞)时,F'(x)<0,F(x)在(e,+∞)上为减函数;(9分)
当x=e时,F(x)
max=F(e)=

(10分)
而G(x)=(x-e)
2+m-e
2 (x>0)
∴G(x)在(0,e)上为减函数,在(e,+∞)上为增函数;(11分)
当x=e时,G(x)
min=m-e
2(12分)
∴当m-
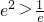
,即m>
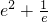
时,方程无解;
当m-
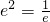
,即m=
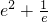
时,方程有一个根;
当m-
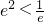
,即m<
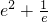
时,方程有两个根;(14分)
分析:(1)因为定义域是实数集R,直接利用奇函数定义域内有0,则f(-0)=-f(0)即f(0)=0,即可求k的值;
(2)先利用函数g(x)的导函数g'(x)=λ+cosx≤0在[-1,1]上恒成立,求出λ的取值范围以及得到g(x)的最大值g(-1)=-1-sin1;然后把g(x)≤t
2+λt+1在x∈[-1,1]上恒成立转化为-λ-sin1≤t
2+λt+1(λ≤-1),整理得(t+1)λ+t
2+sin1+1≥0(λ≤-1)恒成立,再利用一次函数的思想方法求解即可.
(3)先把方程转化为

=x
2-2ex+m,令F(x)=

(x>0),G(x)=x
2-2ex+m (x>0),再利用导函数分别求出两个函数的单调区间,进而得到两个函数的最值,比较其最值即可得出结论.
点评:本题主要考查函数奇偶性的性质,函数恒成立问题以及导数在最大值、最小值问题中的应用,是对知识的综合考查,属于难题.
在涉及到奇函数定义域内有0时,一般利用结论f(0)=0来作题.

 的根的个数.
的根的个数.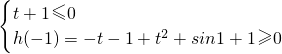 解得t≤-1
解得t≤-1 =x2-2ex+m,令F(x)=
=x2-2ex+m,令F(x)= (x>0),G(x)=x2-2ex+m (x>0),(8分)
(x>0),G(x)=x2-2ex+m (x>0),(8分) ,令F'(x)=0,即
,令F'(x)=0,即 =0,得x=e
=0,得x=e (10分)
(10分)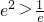 ,即m>
,即m>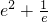 时,方程无解;
时,方程无解;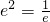 ,即m=
,即m=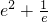 时,方程有一个根;
时,方程有一个根;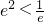 ,即m<
,即m<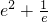 时,方程有两个根;(14分)
时,方程有两个根;(14分) =x2-2ex+m,令F(x)=
=x2-2ex+m,令F(x)= (x>0),G(x)=x2-2ex+m (x>0),再利用导函数分别求出两个函数的单调区间,进而得到两个函数的最值,比较其最值即可得出结论.
(x>0),G(x)=x2-2ex+m (x>0),再利用导函数分别求出两个函数的单调区间,进而得到两个函数的最值,比较其最值即可得出结论.

 名题金卷系列答案
名题金卷系列答案