
【题目】已知U=R且A={x|a2x2-5ax-6<0},B{x||x-2|≥1}.
(1)若a=1,求(UA)![]() B;
B;
(2)求不等式a2x2-5ax-6<0(a∈R)的解集.
【答案】(1){x|x≤-1或x≥6};(2)a=0时,不等式的解集为R;a>0时,不等式的解集为(-![]() ,
,![]() );a<0时,不等式的解集为(
);a<0时,不等式的解集为(![]() ,-
,-![]() ).
).
【解析】
(1)解不等式求出集合![]() ,
,![]() ,再由集合运算法则计算.
,再由集合运算法则计算.
(2)分类讨论,![]() ,
,![]() 时,方程
时,方程![]() 两根为
两根为![]() 和
和![]() ,按它们的大小分类得解集.
,按它们的大小分类得解集.
(1)a=1时,A={x|x2-5x-6<0}={x|-1<x<6},B={x||x-2|≥1}={x|x≤1或x≥3};
∴UA={x|x≤-1或x≥6},
则(UA)![]() B={x|x≤-1或x≥6};
B={x|x≤-1或x≥6};
(2)a=0时,不等式化为-6<0,解集为R;
当a≠0时,不等式化为(ax+1)(ax-6)<0,即(x+![]() )(x-
)(x-![]() )<0;
)<0;
若a>0,则-![]() <
<![]() ,不等式的解集为(-
,不等式的解集为(-![]() ,
,![]() );
);
若a<0,则-![]() >
>![]() ,不等式的解集为(
,不等式的解集为(![]() ,-
,-![]() );
);
综上知,a=0时,不等式的解集为R;
a>0时,不等式的解集为(-![]() ,
,![]() );
);
a<0时,不等式的解集为(![]() ,-
,-![]() ).
).


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,
两点,![]() 不与
不与![]() 轴垂直,圆
轴垂直,圆![]() .
.
(1)若点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在圆
在圆![]() 上,求
上,求![]() 的最大值;
的最大值;
(2)若过线段![]() 的中点
的中点![]() 且垂直于
且垂直于![]() 的直线
的直线![]() 过点
过点![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等轴双曲线![]() :
:![]() 的右焦点为
的右焦点为![]() ,
,![]() 为坐标原点,过
为坐标原点,过![]() 作一条渐近线的垂线
作一条渐近线的垂线![]() 且垂足为
且垂足为![]() ,
,![]() .
.
(1)求等轴双曲线![]() 的方程;
的方程;
(2)若过点![]() 且方向向量为
且方向向量为![]() 的直线
的直线![]() 交双曲线
交双曲线![]() 于
于![]() 、
、![]() 两点,求
两点,求![]() 的值;
的值;
(3)假设过点![]() 的动直线
的动直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,试问:在
两点,试问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为常数,若存在,求出
为常数,若存在,求出![]() 的坐标,若不存在,试说明理由.
的坐标,若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季取暖时减少能源消耗,业主决定对房屋的屋顶和外墙喷涂某种新型隔热材料,该材料有效使用年限为20年.已知房屋外表喷一层这种隔热材料的费用为每毫米厚6万元,且每年的能源消耗费用![]() (万元)与隔热层厚度
(万元)与隔热层厚度![]() (毫米)满足关系:
(毫米)满足关系:![]() .设
.设![]() 为隔热层建造费用与
为隔热层建造费用与![]() 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)请解释![]() 的实际意义,并求
的实际意义,并求![]() 的表达式;
的表达式;
(2)当隔热层喷涂厚度为多少毫米时,业主所付的总费用![]() 最少?并求此时与不建隔热层相比较,业主可节省多少钱?
最少?并求此时与不建隔热层相比较,业主可节省多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子商务平台的管理员随机抽取了1000位上网购物者,并对其年龄(在10岁到69岁之间)进行了调查,统计情况如下表所示.
年龄 |
|
|
|
|
|
|
人数 | 100 | 150 |
| 200 |
| 50 |
已知![]() ,
,![]() ,
,![]() 三个年龄段的上网购物的人数依次构成递减的等比数列.
三个年龄段的上网购物的人数依次构成递减的等比数列.
(1)求![]() 的值;
的值;
(2)若将年龄在![]() 内的上网购物者定义为“消费主力军”,其他年龄段内的上网购物者定义为“消费潜力军”.现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,再从这5人中抽取2人,求这2人中至少有一人是消费潜力军的概率.
内的上网购物者定义为“消费主力军”,其他年龄段内的上网购物者定义为“消费潜力军”.现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,再从这5人中抽取2人,求这2人中至少有一人是消费潜力军的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某地区年龄在25~55岁的人员中,随机抽出100人,了解他们对今年两会的热点问题的看法,绘制出频率分布直方图如图所示,则下列说法正确的是( )
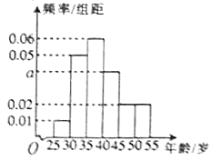
A. 抽出的100人中,年龄在40~45岁的人数大约为20
B. 抽出的100人中,年龄在35~45岁的人数大约为30
C. 抽出的100人中,年龄在40~50岁的人数大约为40
D. 抽出的100人中,年龄在35~50岁的人数大约为50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com