练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】函数y= 的值域为

    【答案】[0，2]
    【解析】解：要使函数y= 的解析式有意义，
    ﹣x2+4≥0，解得：﹣2≤x≤2，
    当x=±2时，﹣x2+4取最小值0，此时函数y= 取最小值0，
    当x=0时，﹣x2+4取最大值4，此时函数y= 取最大值2，
    故函数y= 的值域为[0，2]，
    所以答案是：[0，2]．
    【考点精析】认真审题，首先需要了解函数的值域(求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的)，还要掌握函数的最值及其几何意义(利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值)的相关知识才是答题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）是定义在R上的偶函数，对任意x∈R，都有f（x+2）=f（x﹣2），且当x∈[﹣2，0]时，f（x）=（ ）x﹣1，若在区间（﹣2，6]内关于x的方程f（x）﹣loga（x+2）=0（a＞1）有3个不同的实数根，则a的取值范围是（ ）
    A.（1，2）
    B.（2，+∞）
    C.（1， ）
    D.（ ，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下表是一位母亲给儿子作的成长记录：

    年龄/周岁

    3

    4

    5

    6

    7

    8

    9

    身高/cm

    94.8

    104.2

    108.7

    117.8

    124.3

    130.8

    139.1

    根据以上样本数据，她建立了身高 （cm）与年龄x（周岁）的线性回归方程为 ，给出下列结论：
    ①y与x具有正的线性相关关系；
    ②回归直线过样本的中心点（42，117.1）；
    ③儿子10岁时的身高是 cm；
    ④儿子年龄增加1周岁，身高约增加 cm.
    其中，正确结论的个数是
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直角梯形中， 点是边的中点，将沿折起，使平面平面,连接得到如图所示的几何体.

    （1）求证; 平面；

    （2）若二面角的平面角的正切值为求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，直线的参数方程为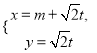（为参数），以坐标原点为极点， 轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，且直线经过曲线的左焦点．

    （1）求直线的普通方程；

    （2）设曲线的内接矩形的周长为，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,已知点P在☉O外,PC是☉O的切线,切点为C,直线PO与☉O相交于点A,B.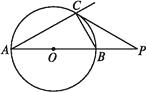

    （1）试探索∠BCP与∠P的数量关系;
    （2）若∠A=30°,则PB与PA有什么关系?
    （3）∠A可能等于45°吗?为什么?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．

    （1）若函数有三个不同的极值点，求的值；

    （2）若存在实数，使对任意的，不等式恒成立，求正整数的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】☉O为△ABC的内切圆,AB=9,BC=8,CA=10,点D,E分别为AB,AC上的点,且DE为☉O的切线,求△ADE的周长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x+ ，且此函数图象过点（1，5）．
    （1）求函数m的值；
    （2）判断函数f（x）在[2，+∞）上的单调性？并证明你的结论．

    查看答案和解析>>

    同步练习册答案