
【题目】已知数列![]() 满足
满足![]() .
.
(1)若![]() ,证明:
,证明:
(i)当![]() 时,有
时,有![]() ;
;
(ii)当![]() 时,有
时,有![]() .
.
(2)若![]() ,证明:当
,证明:当![]() 时,有
时,有![]() .
.
【答案】(1)(ⅰ)见解析;(ⅱ)见解析;(2)见解析.
【解析】
因为![]() ,
,
所以,![]() ,即数列
,即数列![]() 为递增数列.
为递增数列.
(1)(ⅰ)由![]() 及
及![]() ,可得
,可得![]() ,
,![]() .
.
于是,当![]() 时,
时,![]() .
.
故![]()
![]() .
.
因此,当![]() 时,
时,![]() .
.
(ⅱ)因为![]() 时,
时,![]() ,
,
所以,![]() ,
,![]() .
.
由![]() ,可得
,可得
![]() .
.
用数学归纳法证明:
![]() .
.
当![]() 时,
时,![]() ,结论成立.
,结论成立.
假设结论对![]() 成立,即
成立,即![]() ,则结合(ⅰ)的结论可得
,则结合(ⅰ)的结论可得
![]() ,
,
即当![]() 时,结论也成立.
时,结论也成立.
综合可知,不等式![]() 对一切
对一切![]() 都成立.
都成立.
因此,当![]() 时,
时,
![]() ,
,
即![]() .
.
又![]() ,
,![]() ,则当
,则当![]() 时,有
时,有
![]() .
.
(2)由于![]() ,而数列
,而数列![]() 为递增数列,故当
为递增数列,故当![]() 时,有
时,有![]() .
.
由![]() ,可得
,可得
![]() .
.
而![]() ,于是,
,于是,

![]() .
.
下面证明:当![]() 时,有
时,有
![]() .
.
根据![]() 及
及![]() ,计算得
,计算得
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() .
.
故当![]() 时,结论成立.
时,结论成立.
假设结论对![]() 成立,即
成立,即
![]() .
.
因为![]() ,而函数
,而函数![]() 在
在![]() 时为增函数,所以,
时为增函数,所以,
![]()
![]() ,
,
即当![]() 时,结论也成立.
时,结论也成立.
综合可知,不等式![]() 对一切
对一切![]() 都成立.
都成立.
于是,当![]() 时,
时,![]() .
.
故![]() .
.
所以,![]() .
.


科目:高中数学 来源: 题型:
【题目】为提高衡水市的整体旅游服务质量,市旅游局举办了旅游知识竞赛,参赛单位为本市内各旅游协会,参赛选手为持证导游.现有来自甲旅游协会的导游3名,其中高级导游2名;乙旅游协会的导游3名,其中高级导游1名.从这6名导游中随机选择2人参加比赛.
(1)求选出的2名都是高级导游的概率;
(2)为了进一步了解各旅游协会每年对本地经济收入的贡献情况,经多次统计得到,甲旅游协会对本地经济收入的贡献范围是![]() (单位:万元),乙旅游协会对本地经济收入的贡献范围是
(单位:万元),乙旅游协会对本地经济收入的贡献范围是![]() (单位:万元),求甲旅游协会对本地经济收入的贡献不低于乙旅游协会对本地经济收入的贡献概率.
(单位:万元),求甲旅游协会对本地经济收入的贡献不低于乙旅游协会对本地经济收入的贡献概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() :实数
:实数![]() 满足不等式
满足不等式![]() ,
,![]() :函数
:函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() 为真命题”是“
为真命题”是“![]() ”的必要不充分条件,求正整数
”的必要不充分条件,求正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数y=f(x),若在其定义域内存在x0,使得x0f(x0)=1成立,则称函数f(x)具有性质M.
(1)下列函数中具有性质M的有____
①f(x)=﹣x+2
②f(x)=sinx(x∈[0,2π])
③f(x)=x![]() ,(x∈(0,+∞))
,(x∈(0,+∞))
④f(x)![]()
(2)若函数f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性质M,则实数a的取值范围是____.
查看答案和解析>>
科目:高中数学 来源: 题型:
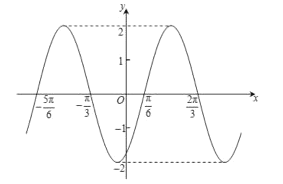
【题目】函数![]() 的图象如图所示,为了得到函数
的图象如图所示,为了得到函数![]() 的图象,可以把函数
的图象,可以把函数![]() 的图象( )
的图象( )
A.先向左平移![]() 个单位,再把所得各点的横坐标伸长到原来的
个单位,再把所得各点的横坐标伸长到原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
B.先向左平移![]() 个单位,再把所得各点的横坐标缩短到原来的
个单位,再把所得各点的横坐标缩短到原来的![]() (纵坐标不变)
(纵坐标不变)
C.每个点的横坐标缩短到原来的![]() (纵坐标不变),再向左平移
(纵坐标不变),再向左平移![]() 个单位
个单位
D.每个点的横坐标伸长到原来的![]() 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移![]() 个单位
个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com