
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ![]() =(1,2)
=(1,2)
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标;
的坐标;
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求v与
垂直,求v与 ![]() 的夹角θ.
的夹角θ.
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< ![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ![]() ,且图象上一个最高点为M(
,且图象上一个最高点为M( ![]() ,3).
,3).
(1)求f(x)的解析式;
(2)先把函数y=f(x)的图象向左平移 ![]() 个单位长度,然后再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,试写出函数y=g(x)的解析式.
个单位长度,然后再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,试写出函数y=g(x)的解析式.
(3)在(2)的条件下,若总存在x0∈[﹣ ![]() ,
, ![]() ],使得不等式g(x0)+2≤log3m成立,求实数m的最小值.
],使得不等式g(x0)+2≤log3m成立,求实数m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=4cos2x﹣4 ![]() sinxcosx的最小正周期为π(>0).
sinxcosx的最小正周期为π(>0).
(1)求的值;
(2)若f(x)的定义域为[﹣ ![]() ,
, ![]() ],求f(x)的最大值与最小值及相应的x的值.
],求f(x)的最大值与最小值及相应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+)(ω>0,0≤≤π)为偶函数,其图象上相邻的两个最高点之间的距离为2π.
(1)求f(x)的解析式;
(2)若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
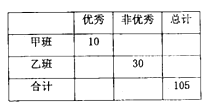
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
已知从全部105人中随机抽取1人为优秀的概率为![]() .
.
(1)请完成上面的列联表:若按![]() 的可靠性要求,根据列联表的数据,能否认为“成绩与班级有关系”;
的可靠性要求,根据列联表的数据,能否认为“成绩与班级有关系”;
(2)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到10号的概率.
附: 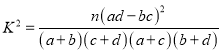

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续航里程数![]() .(单位:公里)分为3类,即
.(单位:公里)分为3类,即![]() 类:
类:![]() ,
,![]() 类:
类:![]() ,
, ![]() 类:
类:![]() ,该公司对这140辆车的行驶总里程进行统计,结果如下表:
,该公司对这140辆车的行驶总里程进行统计,结果如下表:
类型 |
|
|
|
已行驶总里程不超过10万公里的车辆数 | 10 | 40 | 30 |
已行驶总里程超过10万公里的车辆数 | 20 | 20 | 20 |
(1)从这140辆汽车中任取一辆,求该车行驶总里程超过10万公里的概率;
(2)公司为了了解这些车的工作状况,决定抽取了14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从![]() 类车中抽取了
类车中抽取了![]() 辆车.
辆车.
①求![]() 的值;
的值;
②如果从这![]() 辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com