Question

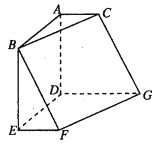
【题目】如图，在六面体中，平面平面， 平面， ， .且， .

（1）求证： 平面；

（2）求锐二面角的余弦值.

Answer 1

【答案】（1）见解析；（2）.

【解析】试题分析：（1）取的中点，连接，通过平行且等于证明是平行四边形，即可证明平行且等于，再证明出是平行四边形，然后根据线面平行判定定理即可求证；（2）由两两垂直，故可建立空间直角坐标系，求出二面角的两个平面法向量，通过计算法向量夹角的余弦值，再根据二面角为锐角即可求出二面角的余弦值.

试题解析：（1）设的中点为，连接， .易证：四边形是平行四边形.

∴，且.

∵平面平面，∴，

∵，∴，且，∴四边形是平行四边形，

∴.又平面， 平面，

故平面.

（2）由题意可得， 两两垂直，故可建立如图所示的空间直角坐标系.

.设平面的法向量为，

则，令，则.

又平面的法向量.

∴ .

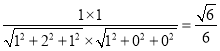由于所求的二面角为锐二面角，∴二面角的余弦值为.